New Blog
I relocated my blog to Hugo due to easier maintainance and more control over content and layout. You can find it here.
All articles from this blog have been preserved, although I won’t list some that I found lacking in quality.
I relocated my blog to Hugo due to easier maintainance and more control over content and layout. You can find it here.
All articles from this blog have been preserved, although I won’t list some that I found lacking in quality.

Combining a deep-depthwise CNN architecture with variable quantization in BitNetMCU achieves state-of-the-art MNIST accuracy on a low-end 32-bit microcontroller with 4 kB RAM and 16 kB flash.
Read the article at my new blog location.
Todays candles have been optimized for millenia not to flicker. But it turns out when we bundle three of them together, we can undo all of these optimizations and the resulting triplet will start to naturally oscillate. A fascinating fact is that the oscillation frequency is rather stable at ~9.9Hz as it mainly depends on gravity and diameter of the flame.
We use a rather unusual approach based on a wire suspended in the flame, that can sense capacitance changes caused by the ionized gases in the flame, to detect this frequency and divide it down to 1Hz.
Candlelight is a curious thing. Candles seem to have a life of their own: the brightness wanders, they flicker, and they react to the faintest motion of air.
There has always been an innate curiosity in understanding how candle flames work and behave. In recent years, people have also extensively sought to emulate this behavior with electronic light sources. I have also been fascinated by this and tried to understand real candles and how artificial candles work.
Now, it’s a curious thing that we try to emulate the imperfections of candles. After all, candle makers have worked for centuries (and millennia) on optimizing candles NOT to flicker?
In essence: The trick is that there is a very delicate balance in how much fuel (the molten candle wax) is fed into the flame. If there is too much, the candle starts to flicker even when undisturbed. This is controlled by how the wick is made.
Now, there is a particularly fascinating effect that has more recently been the subject of publications in scientific journals12 : When several candles are brought close to each other, they start to “communicate” and their behavior synchronizes. The simplest demonstration is to bundle three candles together; they will behave like a single large flame.
So, what happens with our bundle of three candles? It will basically undo millennia of candle technology optimization to avoid candle flicker. If left alone in motionless air, the flames will suddenly start to rapidly change their height and begin to flicker. The image below shows two states in that cycle.

Two states of the oscillation cycle in bundled candles
We can also record the brightness variation over time to understand this process better. In this case, a high-resolution ambient light sensor was used to sample the flicker over time. (This was part of more comprehensive set experiments of conducted a while ago, which are still unpublished)
Plotting the brightness evolution over time shows that the oscillations are surprisingly stable, as shown in the image below. We can see a very nice sawtooth-like signal: the flame slowly grows larger until it collapses and the cycle begins anew. You can see a video of this behavior here. (Which, unfortunately cannot embed properly due to WordPress…)

Left: Brightness variation over time showing sawtooth pattern.
Right: Power spectral density showing stable 9.9 Hz frequency
On the right side of the image, you can see the power spectral density plot of the brightness signal on the left. The oscillation is remarkably stable at a frequency of 9.9 Hz.
This is very curious. Wouldn’t you expect more chaotic behavior, considering that everything else about flames seems so random?
The phenomenon of flame oscillations has baffled researchers for a long time. Curiously, they found that the oscillation frequency of a candle flame (or rather a “wick-stabilized buoyant diffusion flame”) depends mainly on just two variables: gravity and the dimension of the fuel source. A comprehensive review can be found in Xia et al.3.
Now that is interesting: gravity is rather constant (on Earth) and the dimensions of the fuel source are defined by the size (diameter) of the candles and possibly their proximity. This leaves us with a fairly stable source of oscillation, or timing, at approximately 10Hz. Could we use the 9.9 Hz oscillation to derive a time base?
Now that we have a source of stable oscillations—remind you, FROM FIRE—we need to convert them into an electrical signal.
The previous investigation of candle flicker was based an I²C-based light sensor to sample the light signal. This provides very high SNR, but is comparatively complex and adds latency.
A phototransistor provides a simpler option. Below you can see the setup with a phototransistor in a 3mm wired package (arrow). Since the phototransistor has internal gain, it provides a much higher current than a photodiode and can be easily picked up without additional amplification.

Phototransistor setup with sensing resistor configuration
The phototransistor was connected via a sensing resistor to a constant voltage source, with the oscilloscope connected across the sensing resistor. The output signal was quite stable and showed a nice ~9.9 Hz oscillation.
In the next step, this could be connected to an ADC input of a microcontroller to process the signal further. But curiously, there is also a simpler way of detecting the flame oscillations.
Capacitive touch peripherals are part of many microcontrollers and can be easily implemented with an integrated ADC by measuring discharge rates versus an integrated pull-up resistor, or by a charge-sharing approach in a capacitive ADC.
While this is not the most obvious way of measuring changes in a flame, it is to be expected to observe some variations. The heated flame with all its combustion products contains ionized molecules to some degree and is likely to have different dielectric properties compared to the surrounding air, which will be observed as either a change of capacitance or increased electrical loss. A quick internet search also revealed publications on capacitance-based flame detectors.
A CH32V003 microcontroller with the CH32fun environment was used for experiments. The set up is shown below: the microcontroller is located on the small PCB to the left. The capacitance is sensed between a wire suspended in the flame (the scorched one) and a ground wire that is wound around the candle. The setup is completed with an LED as an output.

Complete capacitive sensing setup with CH32V003 microcontroller, candle triplet and a LED.
Initial attempts with two wires in the flame did not yield better results and the setup was mechanically much more unstable.
Read out was implemented straightforward using the TouchADC function that is part of CH32fun. This function measures the capacitance on an input pin by charging it to a voltage and measuring voltage decay while it is discharged via a pull-up/pull-down resistor. To reduce noise, it was necessary to average 32 measurements.
// Enable GPIOD, C and ADC RCC->APB2PCENR |= RCC_APB2Periph_GPIOA | RCC_APB2Periph_GPIOD | RCC_APB2Periph_GPIOC | RCC_APB2Periph_ADC1; InitTouchADC(); ... int iterations = 32; sum = ReadTouchPin( GPIOA, 2, 0, iterations );
First attempts confirmed to concept to work. The sample trace below shows sequential measurements of a flickering candle until it was blown out at the end, as signified by the steep drop of the signal.
The signal is noisier than the optical signal and shows more baseline wander and amplitude drift—but we can work with that. Let’s put it all together.

Capacitive sensing trace showing candle oscillations and extinction
Additional digitial signal processing is necessary to clean up the signal and extract a stable 1 Hz clock reference.
The data traces were recorded with a Python script from the monitor output and saved as csv files. A separate Python script was used to analyze the data and prototype the signal processing chain. The sample rate is limited to around ~90 Hz due to the overhead of printing data via the debug output, but the data rate turned out to be sufficient for this case.

The image above shows an overview of the signal chain. The raw data (after 32x averaging) is shown on the left. The signal is filtered with an IIR filter to extract the baseline (red). The middle figure shows the signal with baseline removed and zero-cross detection. The zero-cross detector will tag the first sample after a negative-to-positive transition with a short dead-time to prevent it from latching to noise. The right plot shows the PSD of the overall and high-pass filtered signal, showing that despite the wandering input signal, we get a sharp ~9.9 Hz peak for the main frequency.
A detailed zoom-in of raw samples with baseline and HP filtered data is shown below.

The inner loop code is shown below, including implementation of IIR filter, HP filter, and zero-crossing detector. Conversion from 9.9 Hz to 1 Hz is implemented using a fractional counter. The output is used to blink the attached LED. Alternatively, an advanced implementation using a software-implemented DPLL might provide a bit more stability in case of excessive noise or missing zero crossings, but this was not attempted for now.
const int32_t led_toggle_threshold = 32768; // Toggle LED every 32768 time units (0.5 second)
const int32_t interval = (int32_t)(65536 / 9.9); // 9.9Hz flicker rate
...
sum = ReadTouchPin( GPIOA, 2, 0, iterations );
if (avg == 0) { avg = sum;} // initialize avg on first run
avg = avg - (avg>>5) + sum; // IIR low-pass filter for baseline
hp = sum - (avg>>5); // high-pass filter
// Zero crossing detector with dead time
if (dead_time_counter > 0) {
dead_time_counter--; // Count down dead time
zero_cross = 0; // No detection during dead time
} else {
// Check for positive zero crossing (sign change)
if ((hp_prev < 0 && hp >= 0)) {
zero_cross = 1;
dead_time_counter = 4;
time_accumulator += interval;
// LED blinking logic using time accumulator
// Check if time accumulator has reached LED toggle threshold
if (time_accumulator >= led_toggle_threshold) {
time_accumulator = time_accumulator - led_toggle_threshold; // Subtract threshold (no modulo)
led_state = led_state ^ 1; // Toggle LED state using XOR
// Set or clear PC4 based on LED state
if (led_state) {
GPIOC->BSHR = 1<<4; // Set PC4 high
} else {
GPIOC->BSHR = 1<<(16+4); // Set PC4 low
}
}
} else {
zero_cross = 0; // No zero crossing
}
}
hp_prev = hp;
Finally, let’s marvel at the result again! You can see the candle flickering at 10 Hz and the LED next to it blinking at 1 Hz! The framerate of the GIF is unfortunately limited, which causes some aliasing. You can see a higher framerate version on YouTube or the original file.
That’s all for our journey from undoing millennia of candle-flicker-mitigation work to turning this into a clock source that can be sensed with a bare wire and a microcontroller. Back to the decade-long quest to build a perfect electronic candle emulation…
All data and code is published in this repository.
This is an entry to the HaD.io “One Hertz Challenge”
 ︎
︎ ︎
︎ ︎
︎LED-based festive decorations are a fascinating subject for exploration of ingenuity in low-cost electronics. New products appear every year and often very surprising technology approaches are used to achieve some differentiation while adding minimal cost.

This year, there wasn’t any fancy new controller, but I was surprised how much the cost of simple light strings was reduced. The LED string above includes a small box with batteries and came in a set of ten for less than $2 shipped, so <$0.20 each. While I may have benefitted from promotional pricing, it is also clear that quite some work went into making the product cheap.
The string is constructed in the same way as one I had analyzed earlier: it uses phosphor-converted blue LEDs that are soldered to two insulated wires and covered with an epoxy blob. In contrast to the earlier device, they seem to have switched from copper wire to cheaper steel wires.
The interesting part is in the control box. It comes with three button cells, a small PCB, and a tactile button that turns the string on and cycles through different modes of flashing and and constant light.


Curiously, there is nothing on the PCB except the button and a device that looks like an LED. Also, note how some “redundant” joints have simply been left unsoldered.
Closer inspection reveals that the “LED” is actually a very small integrated circuit packaged in an LED package. The four pins are connected to the push button, the cathode of the LED string, and the power supply pins. I didn’t measure the die size exactly, but I estimate that it is smaller than 0.3×0.2 mm² = ~0.1 mm².


What is the purpose of packaging an IC in an LED package? Most likely, the company that made the light string is also packaging their own LEDs, and they saved costs by also packaging the IC themselves—in a package type they had available.

I characterized the current-voltage behavior of IC supply pins with the LED string connected. The LED string started to emit light at around 2.7V, which is consistent with the forward voltage of blue LEDs. The current increased proportionally to the voltage, which suggests that there is no current limit or constant current sink in the IC – it’s simply a switch with some series resistance.


Left: LED string in “constantly on” mode. Right: Flashing
Using an oscilloscope, I found that the string is modulated with an on-off ratio of 3:1 at a frequency if ~1.2 kHz. The image above shows the voltage at the cathode, the anode is connected to the positive supply. This is most likely to limit the current.
All in all, it is rather surprising to see an ASIC being used when it barely does more than flashing the LED string. It would have been nice to see a constant current source to stabilize the light levels over the lifetime of the battery and maybe more interesting light effects. But I guess that would have increased the cost of the ASIC too much and then using an ultra-low cost microcontroller may have been cheaper. This almost calls for a transplant of a MCU into this device…

Going along with implementing a very size optimized neural network on a 3 cent microcontroller I created an interactive simulation of a similar network.
You can draw figures on a 8×8 pixel grid and view how the activations propagate through the multi-layer perception network to classify the image into 4 or 10 different numbers. You can find the visualizer online here.
Amazingly, the accuracy is still quite acceptable, even though this network (2 hidden layers with 10 neurons) is even simpler than the one implemented in the 3 cent MCU (3 hidden layers with 16 neurons). One change that led to significant improvements was to use layernorm, which normalizes mean and stddev, instead of RMSnorm, which only normalizes the stddeviation.
Source for React app and training code can be found here. This program was almost exclusively created by prompting with 3.5-Sonnet in the Claude interface and GH Copilot.

Going along with implementing a very size optimized neural network on a 3 cent microcontroller I created an interactive simulation of a similar network.
You can draw figures on a 8×8 pixel grid and view how the activations propagate through the multi-layer perception network to classify the image into 4 or 10 different numbers. You can find the visualizer online here.
Amazingly, the accuracy is still quite acceptable, even though this network (2 hidden layers with 10 neurons) is even simpler than the one implemented in the 3 cent MCU (3 hidden layers with 16 neurons). One change that led to significant improvements was to use layernorm, which normalizes mean and stddev, instead of RMSnorm, which only normalizes the stddeviation.
Source for React app and training code can be found here. This program was almost exclusively created by prompting with 3.5-Sonnet in the Claude interface and GH Copilot.
Bouyed by the surprisingly good performance of neural networks with quantization aware training on the CH32V003, I wondered how far this can be pushed. How much can we compress a neural network while still achieving good test accuracy on the MNIST dataset? When it comes to absolutely low-end microcontrollers, there is hardly a more compelling target than the Padauk 8-bit microcontrollers. These are microcontrollers optimized for the simplest and lowest cost applications there are. The smallest device of the portfolio, the PMS150C, sports 1024 13-bit word one-time-programmable memory and 64 bytes of ram, more than an order of magnitude smaller than the CH32V003. In addition, it has a proprieteray accumulator based 8-bit architecture, as opposed to a much more powerful RISC-V instruction set.

Is it possible to implement an MNIST inference engine, which can classify handwritten numbers, also on a PMS150C?
On the CH32V003 I used MNIST samples that were downscaled from 28×28 to 16×16, so that every sample take 256 bytes of storage. This is quite acceptable if there is 16kb of flash available, but with only 1 kword of rom, this is too much. Therefore I started with downscaling the dataset to 8×8 pixels.

The image above shows a few samples from the dataset at both resolutions. At 16×16 it is still easy to discriminate different numbers. At 8×8 it is still possible to guess most numbers, but a lot of information is lost.
Suprisingly, it is still possible to train a machine learning model to recognize even these very low resolution numbers with impressive accuracy. It’s important to remember that the test dataset contains 10000 images that the model does not see during training. The only way for a very small model to recognize these images accurate is to identify common patterns, the model capacity is too limited to “remember” complete digits. I trained a number of different network combinations to understand the trade-off between network memory footprint and achievable accuracy.

The plot above shows the result of my hyperparameter exploration experiments, comparing models with different configurations of weights and quantization levels from 1 to 4 bit for input images of 8×8 and 16×16. The smallest models had to be trained without data augmentation, as they would not converge otherwise.
Again, there is a clear relationship between test accuracy and the memory footprint of the network. Increasing the memory footprint improves accuracy up to a certain point. For 16×16, around 99% accuracy can be achieved at the upper end, while around 98.5% is achieved for 8×8 test samples. This is still quite impressive, considering the significant loss of information for 8×8.
For small models, 8×8 achieves better accuracy than 16×16. The reason for this is that the size of the first layer dominates in small models, and this size is reduced by a factor of 4 for 8×8 inputs.
Surprisingly, it is possible to achieve over 90% test accuracy even on models as small as half a kilobyte. This means that it would fit into the code memory of the microcontroller! Now that the general feasibility has been established, I needed to tweak things further to accommodate the limitations of the MCU.
Since the RAM is limited to 64 bytes, the model structure had to use a minimum number of latent parameters during inference. I found that it was possible to use layers as narrow as 16. This reduces the buffer size during inference to only 32 bytes, 16 bytes each for one input buffer and one output buffer, leaving 32 bytes for other variables. The 8×8 input pattern is directly read from the ROM.
Furthermore, I used 2-bit weights with irregular spacing of (-2, -1, 1, 2) to allow for a simplified implementation of the inference code. I also skipped layer normalization and instead used a constant shift to rescale activations. These changes slightly reduced accuracy. The resulting model structure is shown below.

All things considered, I ended up with a model with 90.07% accuracy and a total of 3392 bits (0.414 kilobytes) in 1696 weights, as shown in the log below. The panel on the right displays the first layer weights of the trained model, which directly mask features in the test images. In contrast to the higher accuracy models, each channel seems to combine many features at once, and no discernible patterns can be seen.
In the first iteration, I used a slightly larger variant of the Padauk Microcontrollers, the PFS154. This device has twice the ROM and RAM and can be reflashed, which tremendously simplifies software development. The C versions of the inference code, including the debug output, worked almost out of the box. Below, you can see the predictions and labels, including the last layer output.

Squeezing everything down to fit into the smaller PMS150C was a different matter. One major issue when programming these devices in C is that every function call consumes RAM for the return stack and function parameters. This is unavoidable because the architecture has only a single register (the accumulator), so all other operations must occur in RAM.
To solve this, I flattened the inference code and implemented the inner loop in assembly to optimize variable usage. The inner loop for memory-to-memory inference of one layer is shown below. The two-bit weight is multiplied with a four-bit activation in the accumulator and then added to a 16-bit register. The multiplication requires only four instructions (t0sn, sl,t0sn,neg), thanks to the powerful bit manipulation instructions of the architecture. The sign-extending addition (add, addc, sl, subc) also consists of four instructions, demonstrating the limitations of 8-bit architectures.
void fc_innerloop_mem(uint8_t loops) {
sum = 0;
do {
weightChunk = *weightidx++;
__asm
idxm a, _activations_idx
inc _activations_idx+0
t0sn _weightChunk, #6
sl a ; if (weightChunk & 0x40) in = in+in;
t0sn _weightChunk, #7
neg a ; if (weightChunk & 0x80) in =-in;
add _sum+0,a
addc _sum+1
sl a
subc _sum+1
... 3x more ...
__endasm;
} while (--loops);
int8_t sum8 = ((uint16_t)sum)>>3; // Normalization
sum8 = sum8 < 0 ? 0 : sum8; // ReLU
*output++ = sum8;
}
In the end, I managed to fit the entire inference code into 1 kilowords of memory and reduced sram usage to 59 bytes, as seen below. (Note that the output from SDCC is assuming 2 bytes per instruction word, while it is only 13 bits).

Success! Unfortunately, there was no rom space left for the soft UART to output debug information. However, based on the verificaiton on PFS154, I trust that the code works, and since I don’t have any specific application in mind, I left it at that stage.
It is indeed possible to implement MNIST inference with good accuracy using one of the cheapest and simplest microcontrollers on the market. A lot of memory footprint and processing overhead is usually spent on implementing flexible inference engines, that can accomodate a wide range of operators and model structures. Cutting this overhead away and reducing the functionality to its core allows for astonishing simplification at this very low end.
This hack demonstrates that there truly is no fundamental lower limit to applying machine learning and edge inference. However, the feasibility of implementing useful applications at this level is somewhat doubtful.
You can find the project repository here.
Bouyed by the surprisingly good performance of neural networks with quantization aware training on the CH32V003, I wondered how far this can be pushed. How much can we compress a neural network while still achieving good test accuracy on the MNIST dataset? When it comes to absolutely low-end microcontrollers, there is hardly a more compelling target than the Padauk 8-bit microcontrollers. These are microcontrollers optimized for the simplest and lowest cost applications there are. The smallest device of the portfolio, the PMS150C, sports 1024 13-bit word one-time-programmable memory and 64 bytes of ram, more than an order of magnitude smaller than the CH32V003. In addition, it has a proprieteray accumulator based 8-bit architecture, as opposed to a much more powerful RISC-V instruction set.

Is it possible to implement an MNIST inference engine, which can classify handwritten numbers, also on a PMS150C?
On the CH32V003 I used MNIST samples that were downscaled from 28×28 to 16×16, so that every sample take 256 bytes of storage. This is quite acceptable if there is 16kb of flash available, but with only 1 kword of rom, this is too much. Therefore I started with downscaling the dataset to 8×8 pixels.

The image above shows a few samples from the dataset at both resolutions. At 16×16 it is still easy to discriminate different numbers. At 8×8 it is still possible to guess most numbers, but a lot of information is lost.
Suprisingly, it is still possible to train a machine learning model to recognize even these very low resolution numbers with impressive accuracy. It’s important to remember that the test dataset contains 10000 images that the model does not see during training. The only way for a very small model to recognize these images accurate is to identify common patterns, the model capacity is too limited to “remember” complete digits. I trained a number of different network combinations to understand the trade-off between network memory footprint and achievable accuracy.

The plot above shows the result of my hyperparameter exploration experiments, comparing models with different configurations of weights and quantization levels from 1 to 4 bit for input images of 8×8 and 16×16. The smallest models had to be trained without data augmentation, as they would not converge otherwise.
Again, there is a clear relationship between test accuracy and the memory footprint of the network. Increasing the memory footprint improves accuracy up to a certain point. For 16×16, around 99% accuracy can be achieved at the upper end, while around 98.5% is achieved for 8×8 test samples. This is still quite impressive, considering the significant loss of information for 8×8.
For small models, 8×8 achieves better accuracy than 16×16. The reason for this is that the size of the first layer dominates in small models, and this size is reduced by a factor of 4 for 8×8 inputs.
Surprisingly, it is possible to achieve over 90% test accuracy even on models as small as half a kilobyte. This means that it would fit into the code memory of the microcontroller! Now that the general feasibility has been established, I needed to tweak things further to accommodate the limitations of the MCU.
Since the RAM is limited to 64 bytes, the model structure had to use a minimum number of latent parameters during inference. I found that it was possible to use layers as narrow as 16. This reduces the buffer size during inference to only 32 bytes, 16 bytes each for one input buffer and one output buffer, leaving 32 bytes for other variables. The 8×8 input pattern is directly read from the ROM.
Furthermore, I used 2-bit weights with irregular spacing of (-2, -1, 1, 2) to allow for a simplified implementation of the inference code. I also skipped layer normalization and instead used a constant shift to rescale activations. These changes slightly reduced accuracy. The resulting model structure is shown below.

All things considered, I ended up with a model with 90.07% accuracy and a total of 3392 bits (0.414 kilobytes) in 1696 weights, as shown in the log below. The panel on the right displays the first layer weights of the trained model, which directly mask features in the test images. In contrast to the higher accuracy models, each channel seems to combine many features at once, and no discernible patterns can be seen.
In the first iteration, I used a slightly larger variant of the Padauk Microcontrollers, the PFS154. This device has twice the ROM and RAM and can be reflashed, which tremendously simplifies software development. The C versions of the inference code, including the debug output, worked almost out of the box. Below, you can see the predictions and labels, including the last layer output.

Squeezing everything down to fit into the smaller PMS150C was a different matter. One major issue when programming these devices in C is that every function call consumes RAM for the return stack and function parameters. This is unavoidable because the architecture has only a single register (the accumulator), so all other operations must occur in RAM.
To solve this, I flattened the inference code and implemented the inner loop in assembly to optimize variable usage. The inner loop for memory-to-memory inference of one layer is shown below. The two-bit weight is multiplied with a four-bit activation in the accumulator and then added to a 16-bit register. The multiplication requires only four instructions (t0sn, sl,t0sn,neg), thanks to the powerful bit manipulation instructions of the architecture. The sign-extending addition (add, addc, sl, subc) also consists of four instructions, demonstrating the limitations of 8-bit architectures.
void fc_innerloop_mem(uint8_t loops) {
sum = 0;
do {
weightChunk = *weightidx++;
__asm
idxm a, _activations_idx
inc _activations_idx+0
t0sn _weightChunk, #6
sl a ; if (weightChunk & 0x40) in = in+in;
t0sn _weightChunk, #7
neg a ; if (weightChunk & 0x80) in =-in;
add _sum+0,a
addc _sum+1
sl a
subc _sum+1
... 3x more ...
__endasm;
} while (--loops);
int8_t sum8 = ((uint16_t)sum)>>3; // Normalization
sum8 = sum8 < 0 ? 0 : sum8; // ReLU
*output++ = sum8;
}
In the end, I managed to fit the entire inference code into 1 kilowords of memory and reduced sram usage to 59 bytes, as seen below. (Note that the output from SDCC is assuming 2 bytes per instruction word, while it is only 13 bits).

Success! Unfortunately, there was no rom space left for the soft UART to output debug information. However, based on the verificaiton on PFS154, I trust that the code works, and since I don’t have any specific application in mind, I left it at that stage.
It is indeed possible to implement MNIST inference with good accuracy using one of the cheapest and simplest microcontrollers on the market. A lot of memory footprint and processing overhead is usually spent on implementing flexible inference engines, that can accomodate a wide range of operators and model structures. Cutting this overhead away and reducing the functionality to its core allows for astonishing simplification at this very low end.
This hack demonstrates that there truly is no fundamental lower limit to applying machine learning and edge inference. However, the feasibility of implementing useful applications at this level is somewhat doubtful.
You can find the project repository here.
The CH32V203 is a 32bit RISC-V microcontroller. In the produt portfolio of WCH it is the next step up from the CH32V003, sporting a much higher clock rate of 144 MHz and a more powerful RISC-V core with RV32IMAC instruction set architecture. The CH32V203 is also extremely affordable, starting at around 0.40 USD (>100 bracket), depending on configuration.
An interesting remark on twitter piqued my interest: Supposedly the listed flash memory size only refers to a fraction that can be accessed with zero waitstate, while the total flash size is even 224kb. The datasheet indeed has a footnote claiming the same. In addition, the RB variant offers the option to reconfigure between RAM and flash, which is rather odd, considering that writing to flash is usually much slower than to RAM.




Then the 224kb number is mentioned in the memory map. Besides the code flash, there is also a 28Kb boot section and additional configurable space. 224 kbyte +28 kbyte+4=256kbyte, which suggests that the total available flash is 256 kbyte and is remapped to different locations of the memory.
All of these are red flags for an architecture where a separate NOR flash die is used to store the code and the main CPU core has a small SRAM that is used as a cache. This configuration was pioneered by Gigadevice and is also famously used by the ESP32 and RP2040 more recently, although that latter two use an external NOR flash device.
Flash memory is quite different from normal CMOS devices as it requires a special gate stack, isolation and much higher voltages. Therefore, integrating flash memory into a CMOS logic die usually requires extra process steps. The added complexity increases when going to smaller technologies nodes. Separating both dies offers the option of using a high density logic process (for example 45 nm) and pairing it with a low-cost off-the-shell NOR flash die.
To confirm my suspicions I decapsulated a CH32V203C8T6 sample, shown above. I heated the package to drive out the resin and then carefully broke the, now brittle, package apart. Already after removing the lead frame, we can cleary see that it contains two dies.

The small die is around 0.5mm² in area. I wasn’t able to completely removed the remaining filler, but we can see that it is an IC with a smaller number of pads, fitting to a serial flash die.

The microcontroller die came out really well. Unfortunately, the photos below are severely limited by my low-cost USB microscope. I hope Zeptobars or others will come up with nicer images at some point.




The die size of ~1.8 mm² is surprisingly small. In fact it is even smaller than the die of the CH32V003 with a die size of ~2.0 mm² according to Zeptobars die shot. Apart from the fact that the flash was moved off-chip, most likely also a much smaller CMOS technology node was used for the CH32V203 than for the V003.
It was quite surprising to find a two-die configuration in such a low-cost device. But obviously, it explains the oddities in the device specification, and it also explains why 144 MHz core clock is possible in this device without wait-states.
What are the repercussions?
Amazingly, it seems that, instead of only 32kb of flash, as listed for the smallest device, a total of 224kb can be used for code and data storage. The datasheet mentions a special “flash enhanced read mode” that can apparently be used to execute code from the extended flash space. It’s not entirely clear what the impact on speed is, though, but that’s certainly an area for exploration.
I also expect this MCU to be highly overclockable, similar to the RP2040.
I have been meaning for a while to establish a setup to implement neural network based algorithms on smaller microcontrollers. After reviewing existing solutions, I felt there is no solution that I really felt comfortable with. One obvious issue is that often flexibility is traded for overhead. As always, for a really optimized solution you have to roll your own. So I did. You can find the project here and a detailed writeup here.

It is always easier to work with a clear challenge: I picked the CH32V003 as my target platform. This is the smallest RISC-V microcontroller on the market right now, addressing a $0.10 price point. It sports 2kb of SRAM and 16kb of flash. It is somewhat unique in implementing the RV32EC instruction set architecture, which does not even support multiplications. In other words, for many purposes this controller is less capable than an Arduino UNO.
As a test subject I chose the well-known MNIST dataset, which consists of images of hand written numbers which need to be classified from 0 to 9. Many inspiring implementation on Arduino exist for MNIST, for example here. In this case, the inference time was 7 seconds and 82% accuracy was achieved.
The idea is to train a neural network on a PC and optimize it for inference on teh CH32V003 while meetings these criteria:
These criteria can be addressed by using a neural network with quantized weights, were each weight is represented with as few bits as possible. The best possible results are achieved when training the network already on quantized weights (Quantization Aware Training) as opposed to quantized a model that was trained with high accuracy weights. There is currently some hype around using Binary and Ternary weights for large language models. But indeed, we can also use these approaches to fit a neural network to a small microcontroller.
The benefit of only using a few bits to represent each weight is that the memory footprint is low and we do not need a real multiplication instruction – inference can be reduced to additions only.
For simplicity reasons, I decided to go for a e network architecture based on fully-connected layers instead of convolutional neural networks. The input images are reduced to a size of 16×16=256 pixels and are then fed into the network as shown below.

The implementation of the inference engine is straightforward since only fully connected layers are used. The code snippet below shows the innerloop, which implements multiplication of 4 bit weights by using adds and shifts. The weights use a one-complement encoding without zero, which helps with code efficiency. One bit, ternary, and 2 bit quantization was implemented in a similar way.
int32_t sum = 0;
for (uint32_t k = 0; k < n_input; k+=8) {
uint32_t weightChunk = *weightidx++;
for (uint32_t j = 0; j < 8; j++) {
int32_t in=*activations_idx++;
int32_t tmpsum = (weightChunk & 0x80000000) ? -in : in;
sum += tmpsum; // sign*in*1
if (weightChunk & 0x40000000) sum += tmpsum<<3; // sign*in*8
if (weightChunk & 0x20000000) sum += tmpsum<<2; // sign*in*4
if (weightChunk & 0x10000000) sum += tmpsum<<1; // sign*in*2
weightChunk <<= 4;
}
}
output[i] = sum;
In addition the fc layers also normalization and ReLU operators are required. I found that it was possible to replace a more complex RMS normalization with simple shifts in the inference. Not a single full 32×32 multiplication is needed for the inference! Having this simple structure for inference means that we have to focus the effort on the training part.
I studied variations of the network with different numbers of bits and different sizes by varying the numer of hidden activiations. To my surprise I found that the accuracy of the prediction is proportional to the total number of bits used to store the weights. For example, when 2 bits are used for each weight, twice the numbers of weights are needed to achieve the same perforemnce as a 4 bit weight network. The plot below shows training loss vs. total number of bits. We can see that for 1-4 bits, we can basically trade more weights for less bits. This trade-off is less efficient for 8 bits and no quantization (fp32).

I further optimized the training by using data augmentation, a cosine schedule and more epochs. It seems that 4 bit weights offered the best trade off.

More than 99% accuracy was achieved for 12 kbyte model size. While it is possible to achiever better accuracy with much larger models, it is significantly more accurate than other on-MCU implementations of MNIST.

The model data is exported to a c-header file for inclusion into the inference code. I used the excellent ch32v003fun environment, which allowed me to reduce overhead to be able to store 12kb of weights plus the inference engine in only 16kb of flash.

There was still enough free flash to include 4 sample images. The inference output is shown above. Execution time for one inference is 13.7 ms which would actually allow to model to process moving image input in real time.
Alternatively, I also tested a smaller model with 4512 2-bit parameters and only 1kb of flash memory footprintg. Despite its size, it still achieves a 94.22% test accuracy and it executes in only 1.88ms.
This was quite a tedious projects, hunting many lost bits and rounding errors. I am quite pleased with the outcome as it shows that it is possible to compress neural networks very significantly with dedicated effort. I learned a lot and am planning to use the data pipeline for more interesting applications.
The WS2812 has been around for a decade and remains highly popular, alongside its numerous clones. The protocol and fundamental features of the device have only undergone minimal changes during that time.
However, during the last few years a new technology dubbed “Gen2 ARGB” emerged for use in RGB-Illumination for PC, which is backed by the biggest motherboard manufacturers in Taiwan. This extension to the WS2812 protocol allows connecting multiple strings in parallel to the same controller in addition to diagnostic read out of the LED string.
Not too much is known about the protocol and the supporting LED. However, recently some LEDs that support a subset of the Gen2 functionality became available as “SK6112”.
I finally got around summarizing the information I compiled during the last two years. You can find the full documentation on Github linked here.

Years ago I spent some time analyzing Candle-Flicker LEDs that contain an integrated circuit to mimic the flickering nature of real candles. Artificial candles have evolved quite a bit since then, now including magnetically actuated “flames”, an even better candle-emulation. However, at the low end, there are still simple candles with candle-flicker LEDs to emulate tea-lights.
I was recently tipped off to an upgraded variant that includes a timer that turns off the candle after it was active for 6h and turns it on again 18h later. E.g. when you turn it on at 7 pm on one day, it would stay active till 1 am and deactive itself until 7 pm on the next day. Seems quite useful, actually. The question is, how is it implemented? I bought a couple of these tea lights and took a closer look.

Nothing special on the outside. This is a typical LED tea light with CR2023 battery and a switch.



On the inside there is not much – a single 5mm LED and a black plastic part for the switch. Amazingly, the switch does now only move one of the LED legs so that it touches the battery. No additional metal parts required beyond the LED. As prevously, there is an IC integrated together with a small LED die in the LED package.

Looking top down through the lens with a microscope we can see the dies from the top. What is curious about the IC is that it rather large, has plenty of unused pads (3 out of 8 used) and seems to have relatively small structures. There are rectangular regular areas that look like memory, there is a large area in the center with small random looking structure, looking like synthesized logic and some part that look like hand-crafted analog. Could this be a microcontroller?
Interestingly, also the positions of the used pads look quite familiar.

The pad-positions correspond exactly to that of the PIC12F508/9, VDD/VSS are bonded for the power supply and GP0 connects to the LED. This pinout has been adopted by the ubiqitous low-cost 8bit OTP controllers that can be found in every cheap piece of chinese electronics nowadays.
Quite curious, so it appears that instead of designing another ASIC with candle flicker functionality and accurate 24h timer they simply used an OTP microcontroller and molded that into the LED. I am fairly certain that this is not an original microchip controller, but it likely is one of many PIC derivatives that cost around a cent per die.


For some quick electrical characterization is connected the LED in series with a 220 Ohm resistor to measure the current transients. This allows for some insight into the internal operation. We can see that the LED is driven in PWM mode with a frequency of around 125Hz. (left picture)
When synchronizing to the rising edge of the PWM signal we can see the current transients caused by the logic on the IC. Whenever a logic gate switches it will cause a small increase in current. We can see that similar patterns repeat at an interval of 1 µs. This suggests that the main clock of the MCU is 1 MHz. Each cycle looks slightly different, which is indicative of a program with varying instruction being executed.

To gain more insights, I measured that LED after it was on for more than 6h and had entered sleep mode. Naturally, the PWM signal from the LED disappeared, but the current transients from the MCU remained the same, suggesting that it still operates at 1 MHz.
Integrating over the waveform allows to calculate the average current consumption. The average voltage was 53mV and thus the average current is 53mV/220Ohn=240µA.
This is a rather high current consumption. Employing a MCU with sleep mode would allow to bring this down significiantly. For example the PFS154 allows for around 1µA idle current, the ATtiny402 even a bit less.
Given a current consumption of 240µA, a CR2032 with a capacity of 220mAh would last around 220/0.240 = 915h or 38 days.
However, during the 6h it is active a current of several mA will be drawn from the battery. Assuming an average current of 2 mA, the battery woudl theoretically last 220mAh/3mA=73h. In reality, this high current draw will reduce its capacity significantly. Assuming 150mAh usable capacity of a low cost battery, we end up with around 50h of active operating time.
Now lets assume we can reduce the idle current consumption from 240µA to 2µA (18h of off time per day), while the active current consumption stays the same (mA for 6h):
a) Daily battery draw of current MCU: 6h*2mA + 18h*240µA = 16.3mAh
b) Optimzed MCU: 6h*2mA + 18h*2µA = 12mAh
Implementing a proper power down mode would therefore allows extending the operating life from 9.2 days to 12.5 days – quite a significant improvement. The main lever is the active consumption, though.
In the year 2023, it appears that investing development costs in a candle-flicker ASIC is no longer the most economical option. Instead, ultra-inexpensive 8-bit OTP microcontrollers seem to be taking over low-cost electronics everywhere.
Is it possible to improve on this candle-LED implementation? It seems so, but this may be for another project.
A while ago, I used transient current analysis to understand the behavior of the WS2812 a bit better (and to play around with my new oscilloscope). One intersting finding was that the translation of the 8 bit input value for the PWM register is mapped in a nonlinear way to the output duty cycle. This behavior is not documented in the data sheet or anywhere else. Reason enough to revisit this topic.

The table and plot above show PWM pulse length of a WS2812S in dependence of the programmed 8 bit PWM set value, as measured previously by transient current analysis. Normally we would expect that the PWM set value is linearily transferred into a duty cycle. A setting of 1 should correspond to a duty cycle of 1/256=0.39%, a value of 64 to 64/256=25%. As seen in the table, the duty cycle is always lower than the expected value. This is especially true for small values. This is also evident from the log-log plot on the right – the dashed lines would be expected for a linear mapping.

For reference, the pulse waveform for a PWM setting of 1 in a WS2812S is shown above. The rise and fall time of the current source is much faster than the pulse length of the PWM signal.
Based on these obvervations one can conclude that the resolution of the PWM engine in the WS2812 is actually 11 bit, and the 8 bit input value is mapped to the PWM value in a nonlinear fashion. This behavior is part of the digital logic of the PWM engine and must therefore have been introduced intentionally into the design.
To allow for the collection of more datapoints and also compare different devices it is necessary to automate the measurement. I decided to measure the actual intensity of the LED light output instead of indirectly analysing the PWM engine.
I used a Rohm BHL1750 digital ambient light sensor (ALS) for this. Sensors of this type work by averaging the measured ambient light over a certain period. This ensures that all high frequency components, such as arising from pulse width modulation, are removed and a true mean value is reported. I used the “high resolution 2” setting, which measures for 120 ms and does therefore integrated over hundrets of PWM cycles.

My measurement set up is shown above. The ambient light sensor can be seen on the left side. Right next to it is the device under test (DUT). A reflector based on white paper was used to ensure that light from the LED reaches the ambient light sensor in a controlled way. To prevent daylight from disturbing the measurement, a light-blocking enclosure was used (a ceramic salad bowl).
Everything is controlled by a Micropython program on a Raspberry Pi Pico. The code is shown below.
import time, array
import rp2
from machine import Pin, I2C
# Control WS2812 using the PIO
# see https://github.com/raspberrypi/pico-micropython-examples/blob/master/pio/pio_ws2812.py
@rp2.asm_pio(sideset_init=rp2.PIO.OUT_LOW, out_shiftdir=rp2.PIO.SHIFT_LEFT, autopull=True, pull_thresh=24)
def ws2812():
T1 = 2
T2 = 5
T3 = 3
wrap_target()
label("bitloop")
out(x, 1) .side(0) [T3 - 1]
jmp(not_x, "do_zero") .side(1) [T1 - 1]
jmp("bitloop") .side(1) [T2 - 1]
label("do_zero")
nop() .side(0) [T2 - 1]
wrap()
# Create the StateMachine with the ws2812 program, output on Pin(15).
sm = rp2.StateMachine(0, ws2812, freq=8_000_000, sideset_base=Pin(15))
# Start the StateMachine, it will wait for data on its FIFO.
sm.active(1)
# Initialize I2C for light sensor
i2c = I2C(0, sda=Pin(20), scl=Pin(21))
BH1750address = 35
leddata = array.array("I",[0xffffff])
ledoff = array.array("I",[0x0])
i2c.readfrom_mem(BH1750address,0x11,2) # high resolution mode 2
time.sleep(0.2)
for i in range(0,256,1):
leddata[0]=(i<<16) # sweep green channel (order is GRB)
sm.put(leddata,8) # output leddata to PIO FIFO
time.sleep(0.3) # wait until two measurements completed (2*120ms)
rawread=i2c.readfrom_mem(BH1750address,0x11,2)
brightness=(rawread[0]<<8) + (rawread[1])
print(f"{i}\t{brightness}")
sm.put(ledoff,8)I have to admit, that I would have scoffed at the idea of using Python on a microcontroller only a few years ago. But Micropython has come a long way, and the combination with the extremely powerful PIO peripheral on the RP2040 allows implementing even very timing critical tasks, such as the WS2812 protocol.

I picked four different LEDs to investigate; two versions of the WS2812B and two clones for reference. Microscopy images are shown above. All of them are based on 5x5mm² packages.
Generally, it appears that the design houses who provide the controller ICs are somewhat independent from the component assembly companies, who combine the IC with LED chips in a package and ship the product. Therefore the same ICs may appear in product of a number of different LED companies.
For each of the four devices, I swept the green LED channel through PWM settings from 0 to 255 and measured resulting light intensity on the ambient light sensor. I only used the green channel, since the ambient light sensor is most sensitive in that wavelength region. White light may have led to excessive self heating of the LED which causes additional nonlinear effects, especially on the red channel.

Raw measurement results are shown above. The y-axis corresponds to the output value of the ALS, the x-axis is the set PWM value. We can see that all device have similar levels of maximum brightness, which reduces the influence of potential nonlinearities in the ambient light sensor.

The measurements sweeps were normalized to a maximum of 1 to be able to directly compare them. A clear deviation of both WS2812 devices becomes visibles: While the SK6812 and the TX1812 map the PWM set value to a brightness value in a strictly linear fashion, the WS2812 shows lower intensities at smaller PWM values.

This is even more obvious in a log-log plot: The WS2812 shows a systematic deviation from a linear intensity mapping. Due to the nonlinear behavior, the dynamic range of intensity is extended to three decades.
This figure also reveals a difference between WS2812-V1 and V5: The V5 will only turn on for PWM values of 3 and above (see arrow), which is caused by the slow-turn-on PWM engine introduced in the V5. Details can be seen in the oscilloscope screenshots below. Instead of instantly turning on the LED, the current is slowly ramped up after a delay. Due to this behavior, the LED does not turn on at all for PWM=1-2, and does only reach maximum current for PWM>7.

This behavior is in contrast to earlier versions of the WS2812, where the LED current is instantly turned on (see image on top of article), and was most likely introduced to improve electromagnic interference issues (EMI). Unfortunately the loss of lower PWM setting was introduced as an undesireable side effect.
The new optical measurements confirm that the WS2812 does NOT map the PWM settings linearily to intensity, and corroberate the observations from transient current analysis where I analyzed the duty cycle of the PWM waveform.
This is most likely an intentionally introduced design feature in the digital control logic, that maps the 8 bit input value to a 11 bit output values that is fed to the PWM. The exponent of the mapping function is relatively low, therefore this feature cannont replace a true gamma correction step with an exponent of e.g. 2.2 or 2.9.
What are the ramifications of this? The benefit of having a lower slope for low brightness values is to increase dimming resolution. The feature extends the dynamic range of the WS2812 to 1:2048, while the clones only support 1:256.
On the other hand, the introduced nonlinearity may lead to errors in color point rendition since the color perception is defined by the relative intensity of R,G,B.
Does the Ws2812 have integrated gamma correction? No, but it has a feature to extend the dynamic range a little. It would be great to have this functionality properly explained in the datasheet.
After being amazed about finding a really clever implementation of powerline controlled LEDs in a low cost RGB “copper string light”, I bought a few other products in hope to find more LEDs with integrated ICs. At less than $4.00 including shipping, this was by far the cheapest LED string I bought. This one did not have any ICs inside, but I was still surprised about finding rather unusual phosphor converted LED technology in it.
The delivery contained an LED string with attached USB controller and a remote control including battery, as seen in the lower part of the vendor image. The upper part seems to be an artistic impression that shows colors that can not be displayed by the string.

Each of the LEDs in the string has one of four fixed colours: Green, Red, Blue, Warm White/Yellow. The remote control allow changing the brightness or activate one of several animated effects. Based on initial observation, the LED brightness can be controlled in two groups: Yellow/Red and Blue/Green.
This can be easily achieved by connecting two groups of LEDs in antiparallel manner so that either polarity of the string will turn one group of LEDs on. Unlikely in the previous string, this does not require the integration of an integrated circuit into each LED.


The controller looks even more sparse than that of the previous light string. Besides an 8 pin microcontroller with PIC-pinout and the essential set of 32.768 kHz crystal and remote control receive there is only one additional IC on board. U1 is marked “H006” and appears to be a full bridge controller that allows to connect the LED string to power in either direction. I have not been able to identify this chip, but it seems to be quite useful. Two pins of the MCU are connected to it.
There is a tiny detail: How do we connect LEDs with different colors in parallel? The emission color of a LED correlates to it’s forward voltage drop. Red LEDs have a forward voltage of less than 2 V, while green and blue LEDs typically have 3V and more. If LEDs with different colors are connected in parallel, only the ones with the lowest forward voltage light up.
This is not the case here, so what is going on? Let’s take a look at the LEDs.








Above are microscope images of all the four LED colors in the string. It appears that standard LEDs in 0603 form factor have been directy connected to the copper wired without any additional integrated circuit or even forward resistor.

Let’s try a little experiment and illuminate the LEDs with a UV-A LED. You can see the results in the image above. The bottom row shows the resulting emissision from unpowered LEDs of the string. We can clearly see that the Red, Green and Yellow LEDs contain a phosphor that is excited by the UV-A and emits visible light even when no current is applied to the LED.
The blue glow in the UV-A LED and the “blob” around the LEDs in the string is caused by flourescence in the Epoxy compound. There is a nice article about this effect here, where emission at 460 nm was observed for excitation at 396 nm in cured Epoxy.
This is pretty cool. All LEDs in the string are based on a blue-light emitting LED chip, but colors other than blue use a phosphor that converts blue light to a different wavelength. Since all LED chips are identical, they also have identical forward voltage and can be connected in parallel. Employing phosphor-converted LEDs avoids the necessity of additional ICs or resistors to adjust for the forward voltage mismatch in the string. (It’s still not good engineering practice, because bad things may happen when there is a temperature differential across the string, but I guess it’s fine for this application.)
White LEDs with phosphor are everywhere, but other colors are somewhat difficult to come by. It’s really amazing to see them popping up in a lowest cost LED string. Personally, I think that the light emitted from the phosphor converted LEDs has a more pleaseant quality than that of directly emitting LEDs, since it is more diffuse and less monochrome. I have not been able to identify a source of 0603 green/red/yellow phosphor converted LEDs, but I hope they become available eventually.
Again, quite a clever solution in a low end product.
As should be obvious from this blog, I am somewhat drawn to clever and minimalistic implementations of consumer electronics. Sometimes quite a bit of ingeniosity is going into making something “cheap”. The festive season is a boon to that, as we are bestowed with the latest innovation in animated RGB Christmas lights. I was obviously intrigued, when I learned from a comment on GitHub about a new type of RGB light chain that was controlled using only the power lines. I managed to score a similar product to analyze it.
The product I found is shown below. It is a remote controlled RGB curtain. There are many similar products out there. What is special about this one, is that there are groups of LEDs with individual color control, allowing not only to set the color globally but also supporting animated color effects. The control groups are randomly distributed across the curtain.

The same type of LEDs also seems to be used in different products, like “rope-light” for outside usage. A common indication for this LED type seems to be the type of remote control being used, that has both color and animation options (see above).
There seems to be an earlier version of similar LEDs (thanks to Harald for the link) that allows changing global color setting in a similar scheme but without the addressability.


Let’s first take a quick look at the controller. The entire device is USB powered. There is a single 8 pin microcontroller with a 32.768kHz quarz. Possibly to enable reliable timing (there is a timer option on the remote controler) and low power operation when the curtain is turned off. The pinout of the MCU seems to follow the PIC12F50x scheme which is also used by many similar devices (e.g. Padauk, Holtek, MDT). The marking “MF2523E” is unfamiliar though and it was not possible to identify the controller. Luckily this is not necessary to analyze the operation. There are two power mosfets which are obviously used to control the LED string. Only two lines connect to the entire string, named L- (GND) and L+.
All 100 (up to 300 in larger versions) LEDs are connected to the same two lines. These types of strings are known as “copper string lights” and you can see how they are made here (Thanks to Harald from µC.net for the link!). It’s obvious that it is easier to change the LED than the string manufacturing process, so any improvement that does not require additional wires (or even a daisy chain connection like WS2812) is much easier to introduce.



Close up images of a single LED are shown above. We can clearly see that there is a small integrated circuit in every lightsource, and three very tiny LED chips.


Trying to break the LED apart to get a better look at the IC surface was not successful, as the package always delaminated between carrer (The tiny pcb on the left) and chips (still embedded in the epoxy diffusor on the right). What can be deduced however, is that the IC is approximatly 0.4 x 0.6 = 0.24 mm² in area. That is actually around the size of a more complex WS2812 controller IC.
Hooking up the LEDs directly to a power supply caused them to turn on white. Curiously there does not seem to be any kind of constant current source in the LEDs. The current changes direclty in proportion to the applied voltage, as shown below. The internal resistance is around 35 Ohms.
This does obviously simplify the IC a lot, since it basically only has to provide a switch instead of a current source like in the WS2812. It also appears that this allows to regulate the overall current consumption of the LED chain from the string controller by changing the string voltage and control settings. The overall current consumption of the curtain is between 300-450 mA, right up to the allowable maximum of power draw of USB2.0. Maybe this seemingly “low quality” solution is a bit more clever than it looks at the first glance. There is a danger of droop of course, if too much voltage is lost over the length of the string.
Luckily, with only two wires involved, analyzing the protocol is not that complex. I simply hooked up one channel of my oscilloscope to the end of the LED string and recorded what happened when I changed the color settings using the remote control.
The scope image above shows the entire control signal sequence when setting all LEDs to “red”. Some initial observations:
Some more experimentation revealed that the communication is based on messages consisting of an address field and a data field. The data transmission is initiated with a single pulse. The count of following pulses indicates the value that is being transmitted using simple linear encoding (Which seems to be similar to what ChayD observed in his string, so possibly the devices are indeeed the same). No binary encoding is used.
Address and data field are separated by a short pause. A longer pause indicates that the message is complete and changes to the LED settings are latched after a certain time has passed.
My findings are summarized in the diagram above. The signal timing seems to be derived from minimum cycle timing of the 32.768kHz Crystal connected to the microcontroller, as one clock cycle equals ~31 µs. Possibly the pulse timing can be shortened a bit, but then one also has to consider that the LED string is basically a huge antenna…
| Address Field | Function |
| 0 | Unused / No Function |
| 1 … 6 | Address one of six LED subgroubs (zones), writes datafield value into RGB Latch. |
| 7 | Address all LEDs at once (broadcast), adds datafield value to RGB latch content. |
| RGB Latch Value | RGB encoding |
| 0 (000) | Turn LEDs off (Black) |
| 1 (001) | Red |
| 2 (010) | Green |
| 3 (011) | Yellow (Red+Green) |
| 4 (100) | Blue |
| 5 (101) | Magenta (Red+Blue) |
| 6 (110) | Cyan (Green+Blue) |
| 7 (111) | White |
The address field can take values between 1 and 7. A total of six different zones can be addressed with addresses 1 to 6. The data that can be transmitted to the LED is fairly limited. It is only possible to turn the red, green and blue channels on or off, realizing 7 primary color combinations and “off”. Any kind of intermediate color gradient has to be generated by quickly changing between color settings.
To aid this, there is a special function when the address is set to 7. In this mode, all zones are addressed at the same time. But instead of writing the content of the data field to the RGB latch, it is added to it. This allows, for example, changing between neighbouring colors in all zones at once, reducing communication overhead.
This feature is extensively used. The trace above sets the string colour to “yellow”. Instead of just encoding it as RGB value “011”, the string is rapibly changed between green and red, by issuing command “7,1” and “7,7” alternatingly. The reason for this is possibly to reduce brightness and total current consumption. Similar approaches can be used for fading between colors and dimming.
Obviously the options for this are limited by protocol speed. A single command can take up to 1.6ms, meaning that complex control schemes including PWM will quickly reduce the maximum attainable refresh rate, leading to visible flicker and “rainbowing”.
It appears that all the light effects in the controller are specifically built around these limitation, e.g. by only fading a single zone at a time and using the broadcast command if all zones need to be changed.
Implementing the control scheme in software is fairly simple. Below you can find code to send out a message on an AVR. The code can be easily ported to anything else. A more efficient implementation would most likely use the UART or SPI to send out codes.
The string is directly connected to a GPIO. Keep in mind that this is at the same time the power supply for the LEDs, so it only works with very short strings. For longer strings an additional power switch, possibly in push-pull configuration (e.g. MOSFET), is required.
#include <avr/io.h>
#include <util/delay.h>
// Send pulse: 31 µs low (off), 31 µs high (on)
// Assumes that LED string is directly connected to PB0
void sendpulse(void) {
DDRB |= _BV(PB0);
PORTB &= ~_BV(PB0);
_delay_us(31);
PORTB |= _BV(PB0);
_delay_us(31);
}
// Send complete command frame
void sendcmd(uint8_t address, uint8_t cmd) {
sendpulse(); // start pulse
for (uint8_t i=0; i<address; i++) {
sendpulse(); }
_delay_us(90);
sendpulse(); // start pulse
for (uint8_t i=0; i<cmd; i++) {
sendpulse(); }
_delay_us(440);
}It seems to be perfectly possible to control the string without elaborate reset sequence. Nevertheless, you can find details about the reset sequence and a software implementation below. The purpose of the reset sequence seems to be to really make sure that all LEDs are turned off. This requires sending everything twice and a sequence of longer duration pulses with nonobvious purpose.
// Emulation of reset sequence
void resetstring(void) {
PORTB &= ~_BV(PB0); // Long power off sequence
_delay_ms(3.28);
PORTB |= _BV(PB0);
_delay_us(280);
for (uint8_t i=0; i<36; i++) { // On-off sequence, purpose unknown
PORTB &= ~_BV(PB0);
_delay_us(135);
PORTB |= _BV(PB0);
_delay_us(135);
}
_delay_us(540);
// turn everything off twice.
// Some LEDs indeed seem to react only to second cycle.
// Not sure whether there is a systematic reason
for (uint8_t i=7; i>0; i--) {
sendcmd(i,0);
}
for (uint8_t i=7; i>0; i--) {
sendcmd(i,0);
}
}Update: To understand the receiver mechanism a bit more and deduce limits for pulse timing I spent some effort on additional measurements. I used a photodiode to measure the optical output of the LEDs.

An exemplary measurement is shown above. Here I am measuring the light output of one LED while I first turn off all groups and then turn them on again (right side). The upper trace shows the intensity of optical output. We can see that the LED is being turned off and on. Not surprisingly, it is also off during “low” pulses since no external power is available. Since the pulses are relatively short this is not visible to the eye.

Taking a closer look at the exact timing of the update reveals that around 65µs pass after the last pulse in the data field until the LED setting is updated. This is an internally generated delay in the LED that is used to detect the end of the data and address field.
To my surprise, I noticed that this delay value is actually dependent on the pulse timing. The timeout delay time is exactly twice as long as the previous “high” period, the time between the last two “low” pulses.
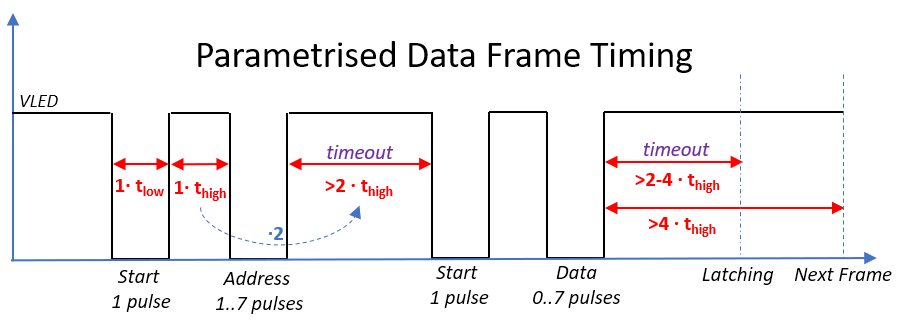
This is shown schematically in the parametrised timing diagram above.
An internal timer measures the duration of the “high” period and replicates it after the next low pulse. Since no clock signal is visible in the supply voltage, we can certainly assume that this is implemented with an analog timer. Most likely a capacitor based integrator that is charged and discharged at different rates. I believe two alternating timers are needed to implement the full functionality. One of them measures the “on”-time, while the other one generates the timeout. Note that the timer is only active when power is available. Counting the pulses is most likely done using an edge detector in static CMOS logic with very low standby power that can be fed from a small on-chip capacitor.
The variable timeout is actually a very clever feature since it allows adjusting the timing over a very wide range. I was able to control the LEDs using pulsewidths as low as 7 µs, a significant speed up over the 31 µs used in the original controller. This design also makes the IC insensitive to process variation, as everything can be implemented using ratiometric component sizing. No trimming is required.
See below for an updated driver function with variable pulse time setting.
#define basetime_us 10
#define frameidle_us basetime_us*5 // cover worst case when data is zero
void sendcmd(uint8_t address, uint8_t cmd) {
for (uint8_t i=0; i<address+1; i++) {
sendpulse();
}
_delay_us((basetime_us*3)/2);
for (uint8_t i=0; i<cmd+1; i++) {
sendpulse();
}
_delay_us(frameidle_us);
}
// Send pulse
void sendpulse(void) {
PORTB &= ~_BV(PB0);
_delay_us(basetime_us);
PORTB |= _BV(PB0);
_delay_us(basetime_us);
}All in all, this is a really clever way to achieve a fairly broad range of control without introducing any additional data signals and while absolutely minimizing the circuit overhead per light source. Of course, this is far from what a WS2812 and clones allow.
Extrapolating from the past means that we should see of more these LEDs at decreasing cost, and who knows what kind of upgrades the next Christmas season will bring.
There seem to be quite a few ways to take this scheme further. For example by finding a more efficient encoding of data or storing further states in the LEDs to enable more finely grained control of fading/dimming. May be an interesting topic to tinker with…

What would it take to build an addressable LED like the WS2812 (aka Neopixel) using only discrete transistors? Time for a small “1960 style logic meets modern application” technology fusion project.

What exactly do we want to build? The diagram above shows how a system with our design would be set up. We have a micontroller with a single data output line. Each “Pixel” module has a data input and a data output than can be used to connect many devices together by “daisy chaining”.
This is basically how the WS2812 works. To simplify things a bit, I had to make some concessions compared to the original WS2812:
The protocol is shown above. “LED Off” is encoded as a short pulse, “LED On” as a long pulse. After the first LED has accepted the data from the first pulse, any subsequent pulses will be forwarded to the next device and so on. This allows programming a chain of TransistorPixels with a train of pulses. If 20µs has passed without any pulse, all devices will reset and are ready to accept new data.
There are many ways to implement the desired functionality. A straightforward but complex way would be to used a clocked logic design. But, of course this is also a challenge in minimalism. Since we are using discrete transistors, we can utilize all kinds of analog circuit tricks. I chose to go with using clockless logic with asynchronous timing elements. The choices in this design may seem obvious in hindsight, but quite some thought went into this.
The schematic above shows the top level architecture of the TransistorPixel. There are three main blocks:
The basic logic style for the circuit is Resistor-Transistor-Logic (RTL). This was the very first transistor based logic style and was, for example, used in the CDC6600 super computer. A benefit of this logic style is that it is very simple and therefore well suitable for small discrete logic designs. There are some drawbacks though, that led to numerous other logic style being developed in later years.
The entire design was first implemented and simulated in LTSpice. You can download the design files from the Hackaday.io project page.

Simulation results from the top level testbench are shown above. You can see the input and output signals of three Pixels and the state of the associated LEDs. Observe how each part of the chain will removed one pulse from the pulse train, use this to turn the LED on or off, and forward the other pulses to the next device. The gap of 20µs between the two trains of pulses is sufficient to reset the receiver so the cycle can start anew.
Below is a photo of the final design implementation. Each block is clearly delineated on the PCB.
Lets review how the individual blocks are implemented.
The data director is a simple multiplexer that consists of two inverters and two NOR gates. The gate symbols along with their respective circuit implementation are shown below. Since two of each are needed, a total of 6 transistors and 10 resistors are used. The beige component is a capacitor that was added for decoupling. I used releatively high base (4.7 kOhm) and collector resistances of (2.2 and 4.7 kOhm) to keep current consumption moderate. The collector resistance has to be adjusted according to the fan-out.
One important aspect is the choice of transistors. Since this is not a super-fast design I chose the PMBT3904, which is a low cost switching transistor. I also tried a chinese clone (The CJ MMBT3904), but encountered issues due to high base charge storage time.
While the design of the data director is straightforward, I encountered some issues with pulse deformation during data forwarding. Since RTL logic operates transistors in the saturating regime, the output delay for a low-high transistion on the input of a gate is much slower than for a high-low transition. This can cause an increase or decrease of pulse length and detoriates the signal during data forwarding. I solved this by ensuring that the signal is fed through two identical inverters in series during data forwarding. This ensures symmatrical timing on rising and falling edge and reduces pulse deformation sufficiently.
The purpose of the state generator is to change the device to the forwarding state after the first pulse has arrived and switch it back to the receiving state when no signal arrived f0r 20µs.
This requirements is met with a retriggerable monoflop that triggers on a falling edge.

The cicuit of the monoflop is shown above. The inverter transforms the falling edge into a rising edge. The rising edge is filtered with C4 and R4 that form a high pass and trigger Q7. If Q7 is turned on, it will discharge C5, which will turn Q8 off and the output of the monoflip is pulled high. C5 is slowely recharged through R6 and will turn on Q8 again after around 20µs.
You can see the output of the state generator above. When the output is high, all input signal will be directed to the output (“datain2”), when it is low, the input will be directed to the receiver.
The decoder and latch unit consists of a non-retriggerable monoflop and a latch that is formed from to NOR-gates. The monoflop triggers on the rising edge of the input signal and will generate an output pulse with a length of approximately 0.6 µs that is fed into the latch. The length of this output pulse is independent of the length of the input pulse. The other input of the latch will directly receive the data signal from the input. When both inputs of the latch are low, the latch will remember the last state of the inputs. Therefore it can discriminate which signal went low first: the reference timing signal from the monoflop or the pulse from the data input. This does effectively allow to discirminate between a pulse that is longer or shorted than the reference. The output of the latch is fed into an additional inverter that serves as a driver for the LED.

The circuit of the non-retriggerable monoflop is shown above. A positive edge on the input of Q2 will pull the collector of Q2 and Q3 down and hence also the base of Q4 through the capacitor. This will pull the output high and turn Q3 on. As long as Q3 is on, further pulses on the base of Q3 are ignored. The monoflop will only turn off once C3 has been recharged via R9. Some more info here. Once interesting aspect of this circuit is that the base of Q4 will be pulled to a negative potential due to capacitive coupling. Hence the stored saturation charge from Q4 is removed much quicker and the output can switch to high with very little delay.
After verification of the design in LTSpice, I created a PCB and used an assembly service to manufacture the PCBs and pick and place the parts. The interesting part is of course, how the actual circuit performs.
A first step was to investigate the timing behavior of the logic gates. The screenshots above show the timing of one of the input inverters base on PMBT3904. The yellow trace corresponds to the input (driven from a MCU GPIO) and the lower channel corresponds to the output. We can see that the propagation time for a L->H transition is 18 ns and for a H->L transition is 162 ns. This is quite some difference to the model I used in LTspice. The main reason for this is that the model used a very pessimistic value for the storage time. After adjusting the storage time parameter (“TR”) to 380 ns, I was able to replicate the behavior of the inverter also in LTspice. The story is a bit different when using chinese clone transistors (CJ MMBT3904). They had a much longer storage time and hence a H->L delay of 283 ns which caused marginal timing. However, it turns out that the circuit does still somewhat work even with the CJ transistors.

Shown above is the input-output relationship when a signal is forwarded through a “Pixel”. The output pulse looks much less steep, thanks due to the slow response of the used RTL gates. However, pulses above 250 ns are still faithfully reproduced, which is sufficient to guaruantee proper operation.
This screenshot shows the behavior of the LED out in relation to input pulses of different length. The upper trace corresponds to the state of the LED (ON/OFF). We can see that a very short pulse of 62.5 ns will not turn off the LED and is ignored. Staring from 125 ns the LED is properly turned off and pulses of 625 ns and above will turn the LED on – as expected.
Not much to say – this was a fun little design that allowed to explore ancient logic styles in a maneagable and purposeful way (ok, at least somewhat…). The interesting challenge is to reduce the number of transistors used. Can you do better? Remember that it has to work in a real circuit, so using idealistic assumptions about the behavior of the transistors may not be sufficient.

Flashing a LED is certainly among the first set of problems any burgeoning electronics specialist is tackling, may it be by using an ancient NE555 or, more recently, a microcontroller to control the LED. As it turns out, we can turn any trivial problem into a harder one by changing its constraints.
So, what about the challenge of flashing a LED from the charge of a single battery as long as possible? Of course, also this is not a novel problem. Two interesting approaches that I came across in the past: 1) Burkhard Kainkas Ewiger Blinker (“Eternal Blinky”) and 2) Ted Yapos TritiLED.
B. Kainkas project is a n LED flasher circuit made from discrete transistors that consumes about 50µA and is able to run for years from a single AA cell. Ted Yapo raised the bar a bit further and investigated in intricate detail how to make a LED shine for years at very low intensity from a CR2032 coin cell. His project logs are worth a read for certain. One very interesting detail is that he concluded that using a lower power microcontroller to control the LED is actually the most efficient option. This may be a bit counterintuitive, but appears more obvious when looking at his attempts of building a discrete version.
Many microcontrollers offer highly optimized low power sleep-modes that can be used to wait between the flashes. The microcontroller will only be active when the LED needs to be flashed. At that point it does not really matter how much the active power consumption of the microcontroller is, because the LED will need several mA to emit light at a sufficient level.
Enter the infamous “3 cent” Padauk microcontroller family that I used for several projects before. To my surprise, these devices offer very competitive low power sleeping modes that seems to be on par with several “low power” 8 bit microcontrollers that cost ten times as much. I investigated how to implement an ultra low power LED flasher on the PFS154.
The first step in reducing the power consumption of the MCU is to use the low speed oscillator as a clock source. In the PFS154 this is called the “ILRC” and provides a clock of around 52 kHz depending on supply voltage. One oddity I found is that it was necessary to activate both the high-speed and low-speed oscillator as a first step and only disable the high speed oscillator in a second step. Directly switching to the ILRC halted the MCU. The code example below is based on the free-pdk includes.
/* Activate low frequency oscillator as main clock. */
CLKMD = CLKMD_ILRC | CLKMD_ENABLE_ILRC | CLKMD_ENABLE_IHRC;
CLKMD = CLKMD_ILRC | CLKMD_ENABLE_ILRC ;
// Note: it is important to turn off IHRC only after clock
// settings have been updated. Otherwise the CPU stalls.

Running the PFS154 at such a low clock will already reduce the power consumption to far below 100 µA. Not all of this is dynamic power consumption that scales with the clock rate, so the only way to go further is to activate one of the sleep modes.
The PFS154 supports two sleep modes: “STOPSYS” and “STOPEXE”.
STOPSYS completely halts the core and all oscillators. The only way to wake up from this state is by a pin change.
STOPEXE halts the core, but the low frequency oscillator remains active and can be used to clock the timers. The core can be woken up by pin change or timer event. It appears that, although not clearly states in the datasheet, both the 8 bit timers and the 16 bit timer can generate wake-up events. Note that the watchdog timer is also halted during STOPEXE. This is on contrast to the behavior on other microcontrollers.

As a first step I used my multimeter to verify the current consumption vs supply voltage during the sleep modes as shown above. I was basically able to reproduce the curves from the datasheet, which confirms that the datasheet is correct and that my handheld multimeter is actually able to accurately measure currents as low as a few 100 nA! Not something I had expected, to be honest.
During this I found one peculiar behavor of the PFS154. The pin change wakeup is always enabled by default after reset. It appears that very low changes on the pins can generate a wakeup. If they are left floating, it is sufficient to touch a pin to wake up the core. Interestingly this even applied to pins that were not routed outside of the package put still existed as pads on the die. By touching the surface of the IC it was possible to generate a wake up event! Unless you are interested in building a hacky touch sensor it is therefore adviced to disable all pins as a wakeup source.
Since I want to build a LED flasher, I used Timer2 to generate a wakeup event at a frequency of around 1.6Hz. You can see the full code for STOPEXE configuration and timer initialization below.
/* Configure STOPEXE mode and set up Timer 2 as wake up source */
PADIER = 0; // disable pins as wakeup source
PBDIER = 0; // Also port B needs to be disabled even if it is
// not connected to the outside of the package.
// Touching the package can introduce glitches and wake
// up the device
INTEN = 0; // Make sure all interrupts are disabled
INTRQ = 0;
MISC = MISC_FAST_WAKEUP_ENABLE;
// Enable faster wakeup (45 clocks instead of 3000)
// This is important to not waste energy, as 40µA bias
// is already added during wakeup time
TM2C = TM2C_CLK_ILRC | TM2C_MODE_PWM;
// Oscilator source for timer 2 is LRC (53 kHZ)
TM2CT = 0;
TM2S = TM2S_PRESCALE_DIV16 | TM2S_SCALE_DIV8;
// Divide clock by 16*7=112 -> 53 kHz / 122 = 414 Hz
TM2B = 1;
// PWM threshold set to 1.
// The PWM event will trigger the wakeup.
// Wakeup occurs with 414 Hz / 256 = 1.66 Hz
One important optimization was to turn on the “fast wakeup mode”. The normal wakeup mode takes around 3000 clocks cycles during which around 40µA of current are consumed. I found that the 8 bit timers can also be used as PWM generators during STOPEXE mode. However it is not possible to prevent them from waking up the CPU, so they cannot be used autonomously.
The only part that remains is the code to actually flash the LED. This is rather simple as shown below.
/* Initialize LED I/O and flash the LED */
PA = 1<<4; // LED is on PA4, set all other output to zero.
PAPH = 0; // Disable all pull up resistors
PAC = 0; // Disable all outputs
// Note: There is no series resistor for the LED
// The LED current is limited LOW IO driving setting
// See Setction 4.14 (p24) in PFS154 manual
// The output is disabled when the LED is off
// to avoid leakage
for (;;) {
PAC |=1<<4;
// Enable LED output (It's set to High)
__nop();
__nop();
__nop();
PAC &=~(1<<4);
// Disable LED output after 4 cycles => 4/53 kHz = 75.5 µS
__stopexe();
}
The processor core will wakeup after every event generated by timer2, turn on the LED for 75.5µS, and put the core to sleep again. The LED is directly connected to an output pin without series resistor while the pin is configured to low I/O driving strength to limit the maximum current. This is somewhat risky, but allows operating the LED down to the lowest possible voltage – around 2.1V for the green LED I am using.
Well, the code works nicely and flashes the LED at 1.6 Hz at voltages down to slightly above 2V. You can find the complete source here.

To evaluate that everything works correctly, I set up a simple power model that considers sleep mode current, active current and the current used by the LED. The LED current was determined by measuring the on current of the LED connected to the microcontroller at different supply voltages and multiplying it by the duty cycle. The same approach was taken for the active current of the MCU. You can see the output of the model above and comparison with a measurements. I had to use a series resistor of a few kilohm and a parallel capacitor to ensure that the current ripple was smoothed enough to allow for a steady reading on the multimeters.
As you can see, there is good agreement between model and measurements. Due to the extremely low duty cycle of the LED, the main power consumption is still the MCU and the timer. This contribution is highly dependent on supply voltage, so that the most energy efficicent operation is achieved at the lowest voltage.
The total current consumption at 3V is only about 1 µA! This is less than the self-discharge current of many batteries. A single CR2023 cell with a capacity of around 200 mAh could theoretically power this flasher for 200000 hours, or 22 years! I was able to operate the circuit (as shown in the title image) for more than 10 minutes based on the charge of a 330µF capacitor charged to 5V.
Despite their low cost, the Padauk MCUs can be used for extremely low power operation. There are certainly ways to improve the flasher circuit more, for example by using an inductive boost converter to allow constant current operation of the LED at even lower voltages.