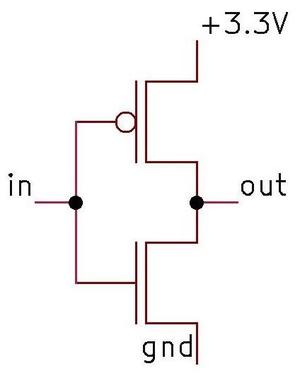
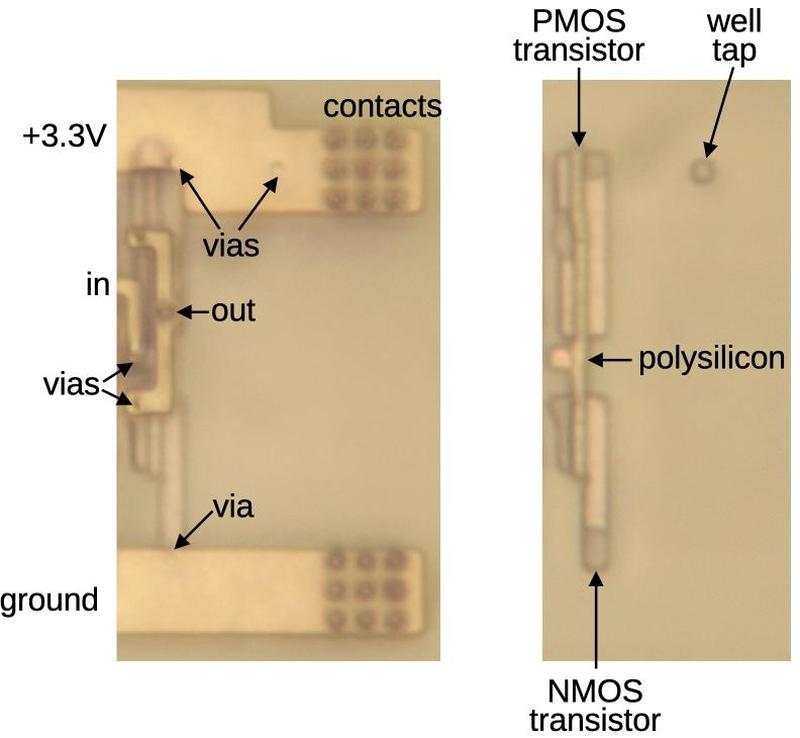
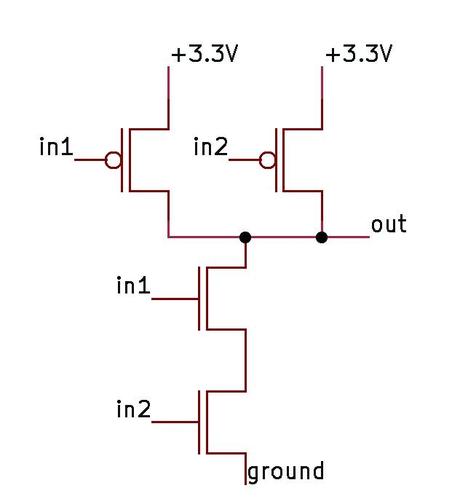
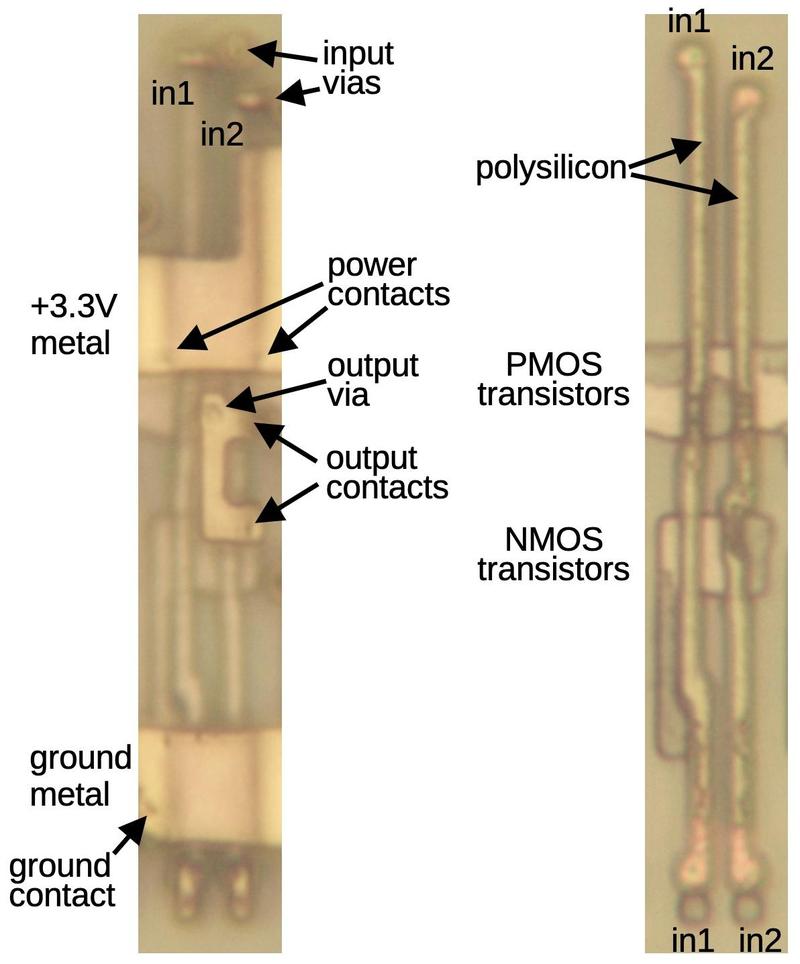
Hurrying through the National Gallery of Art five minutes before closing, I passed a Navajo weaving with a complex abstract
pattern.
Suddenly, I realized the pattern was strangely familiar, so I stopped and looked closely.
The design turned out to be an image of Intel's Pentium chip, the start of the long-lived Pentium family.1
The weaver, Marilou Schultz, created the artwork in 1994 using traditional materials and techniques.
The rug was commissioned by Intel as a gift to AISES (American Indian Science & Engineering Society) and
is currently part of an art exhibition—Woven Histories: Textiles and Modern Abstraction—focusing on the intersection between abstract art and woven textiles.

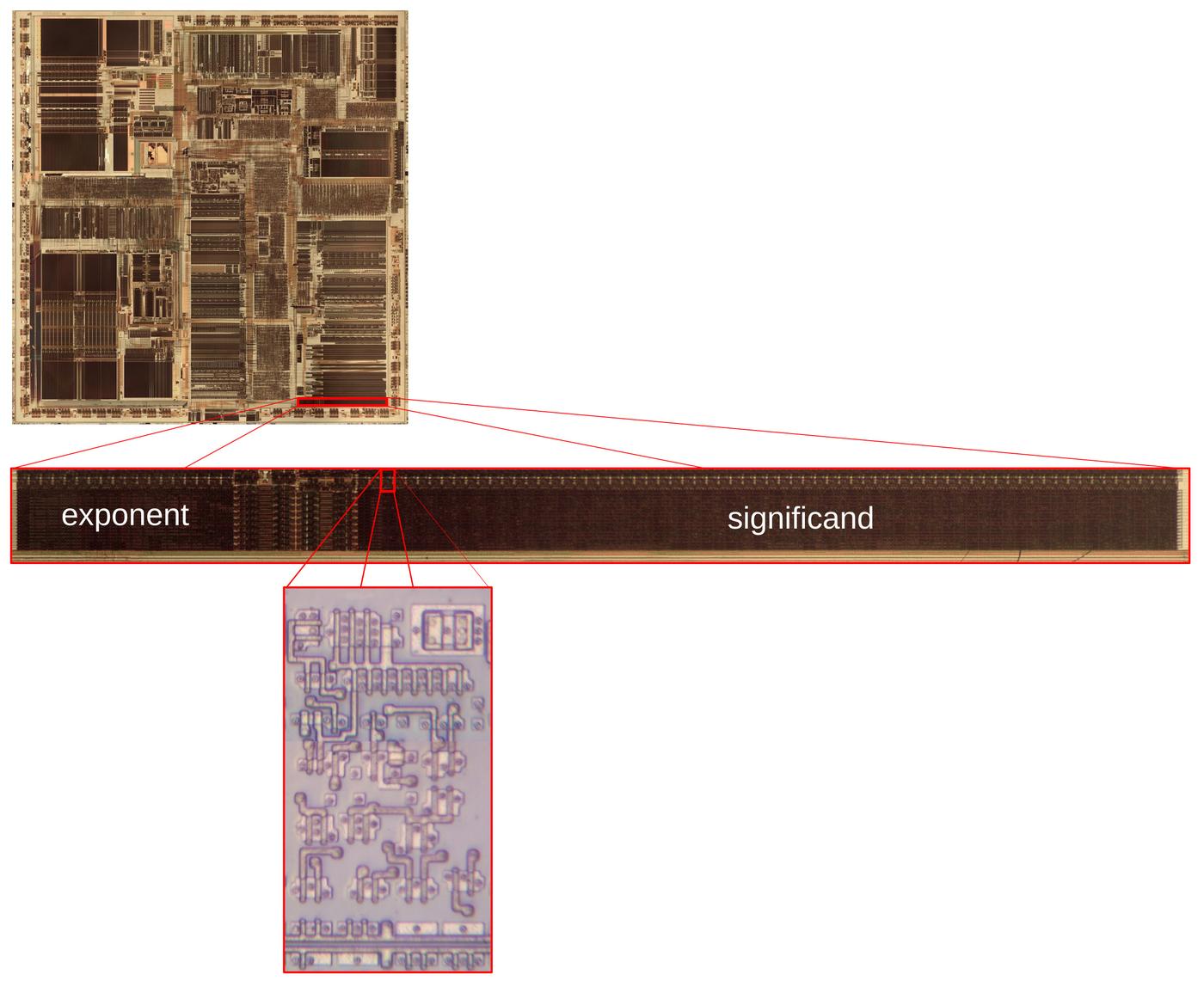
"Replica of a Chip", created by Marilou Schultz, 1994. Wool. Photo taken at the National Gallery of Art, 2024.
I talked with Marilou Schultz, a Navajo/Diné weaver and math teacher, to learn more about the artwork.
Schultz learned weaving as a child—part of four generations of weavers—carding the wool, spinning it into yarn, and then weaving it.
For the Intel project, she worked from a photograph of the die, marking it into 64 sections along each side so the die pattern could be
accurately transferred to the weaving.
Schultz used the "raised outline" technique, which gives a three-dimensional effect along borders.
One of the interesting characteristics of the Pentium from the weaving perspective is its lack of symmetry, unlike traditional rugs.
The Pentium weaving was colored with traditional plant dyes;
the cream regions are the natural color of the
wool from the long-horned Navajo-Churro sheep.2
The yarn in the weaving is a bit finer than the yarn typically used for knitting.
Weaving was a slow process, with a day's work extending the rug by 1" to 1.5".
The Pentium die photo below shows the patterns and structures on the surface of the fingernail-sized silicon die, over
three million tiny transistors.
The weaving is a remarkably accurate representation of the die,
reproducing the processor's complex designs.
However, I noticed that the weaving was a mirror image of the physical Pentium die; I had to flip the rug image below to make them match.
I asked Ms. Schultz if this was an artistic decision and she explained that she wove the rug to match the photograph.
There is no specific front or back to a Navajo weaving because the design is similar on both sides,3
so the gallery picked an arbitrary side to display.
Unfortunately, they picked the wrong side, resulting in a backward die image. This probably bothers nobody but me, but I
hope the gallery will correct this in future exhibits.
For the remainder of this article, I will mirror the rug to match the physical die.

Comparison of the Pentium weaving (flipped vertically) with a Pentium die photo. Original die photo from
Intel.
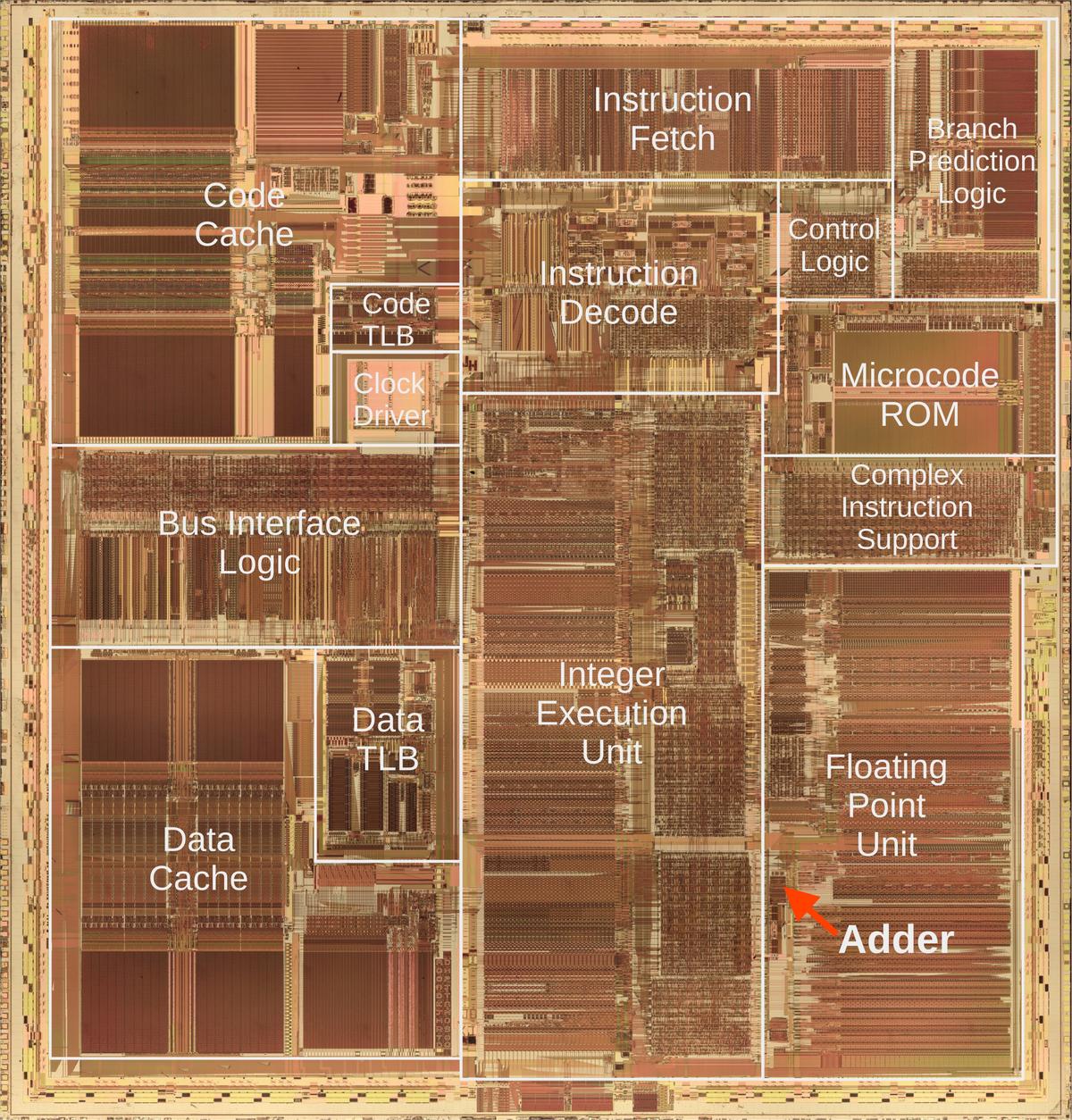
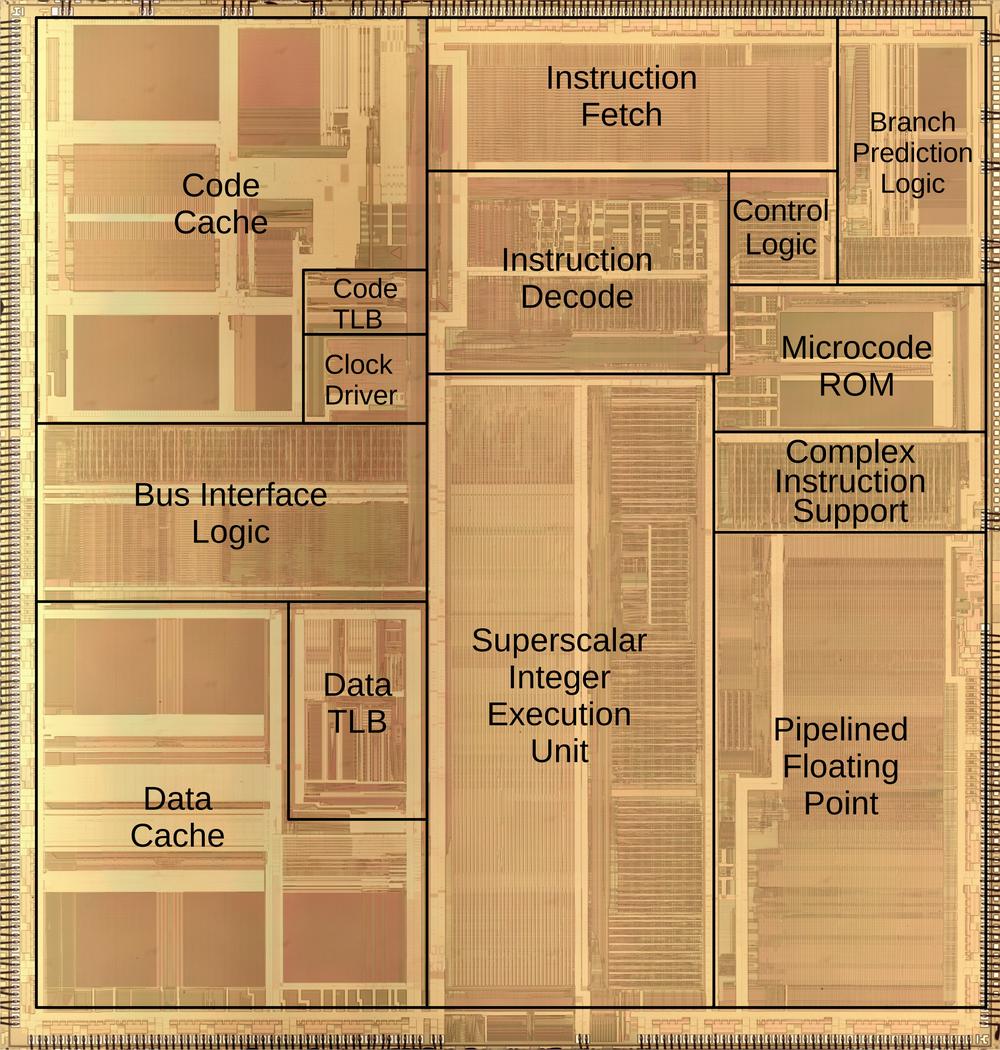
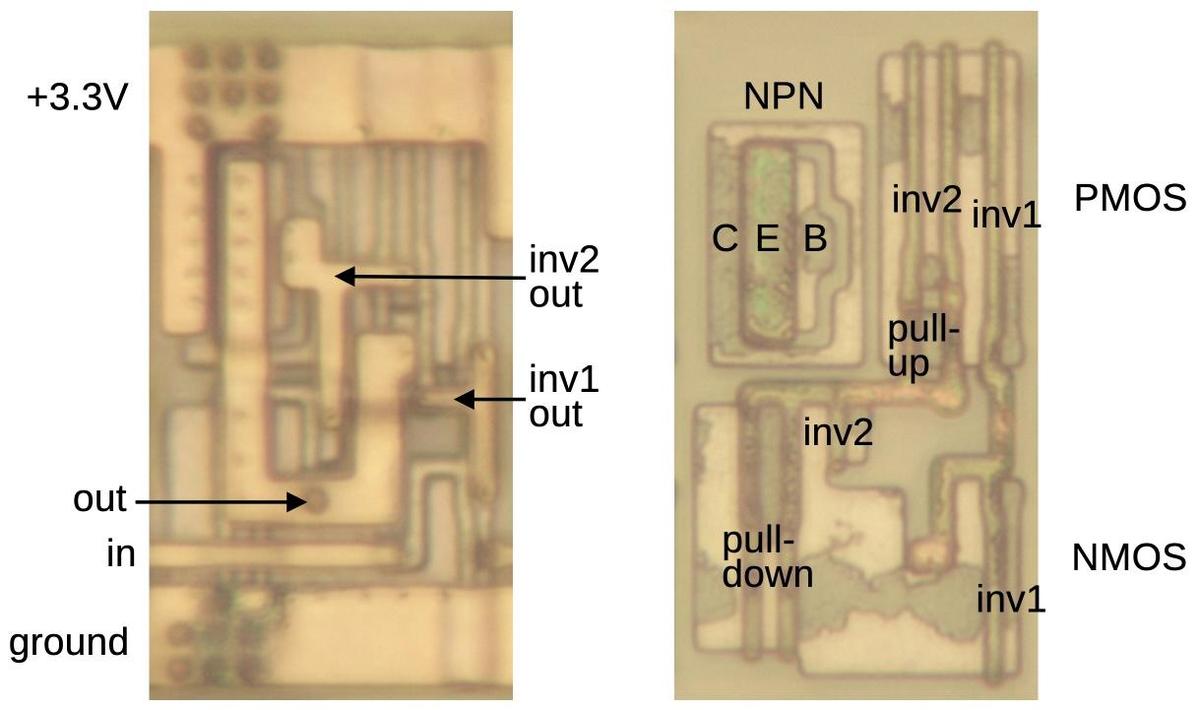
The rug is accurate enough that each region can be marked with its corresponding function in the real chip, as shown below.
Starting in the center, the section labeled "integer execution units" is the heart of the processor, performing
arithmetic operations and other functions on integer numbers.
The Pentium is a 32-bit processor, so the integer execution unit is a vertical rectangle, 32 bits wide.
The horizontal lines correspond to different types of circuitry such as adders, multipliers, shifters, and registers.
To the right, the "floating point unit" performs more complex arithmetic operations on floating-point numbers,
numbers with a fractional part that are used in applications such as spreadsheets and CAD drawings.
Like the integer execution unit, the floating point unit has horizontal stripes corresponding to different functions.
Floating-point numbers are represented with more bits, so the stripes are wider.
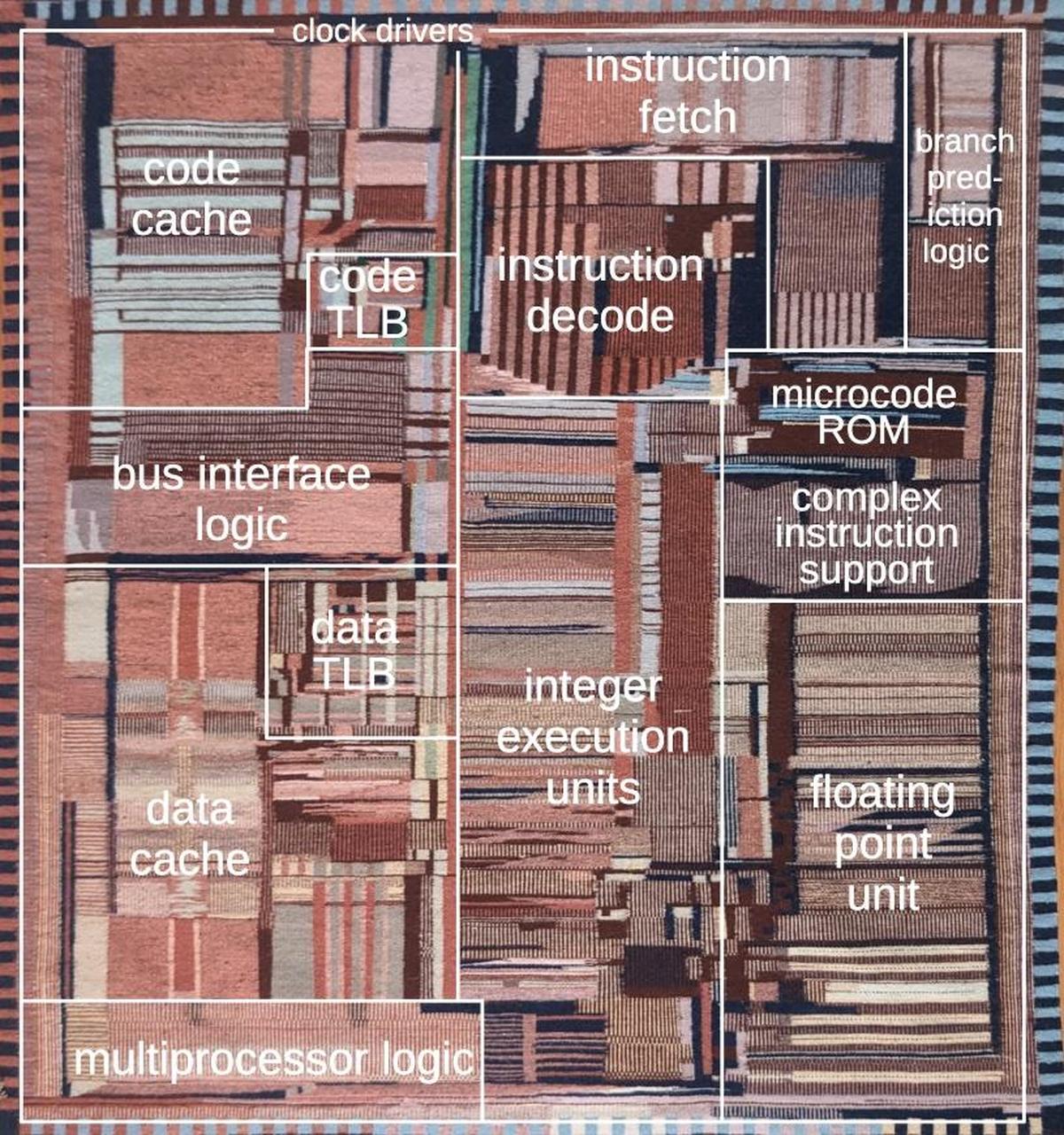
The Pentium weaving, flipped and marked with the chip floorplan.
At the top, the "instruction fetch" section fetches the machine instructions that make up the software.
The "instruction decode" section analyzes each instruction to determine what operations to perform.
Simple operations, such as addition, are performed directly by the integer execution unit.
Complicated instructions (a hallmark of Intel's processors) are broken down into
smaller steps by the "complex instruction support" circuitry, with the steps held in the "microcode ROM".
The "branch prediction logic" improves performance when the processor must make a decision for a branch instruction.
The code and data caches provide a substantial performance boost.
The problem is that the processor is considerably faster than the computer's RAM memory, so the processor can end up sitting idle until program
code or data is provided by memory.
The solution is the cache, a small, fast memory that holds bytes that the processor is likely to need.
The Pentium processor had a small cache by modern standards, holding 8 kilobytes of code and 8 kilobytes of data.
(In comparison, modern processors have multiple caches, with hundreds of kilobytes in the fastest cache and megabytes in a slower
cache.)
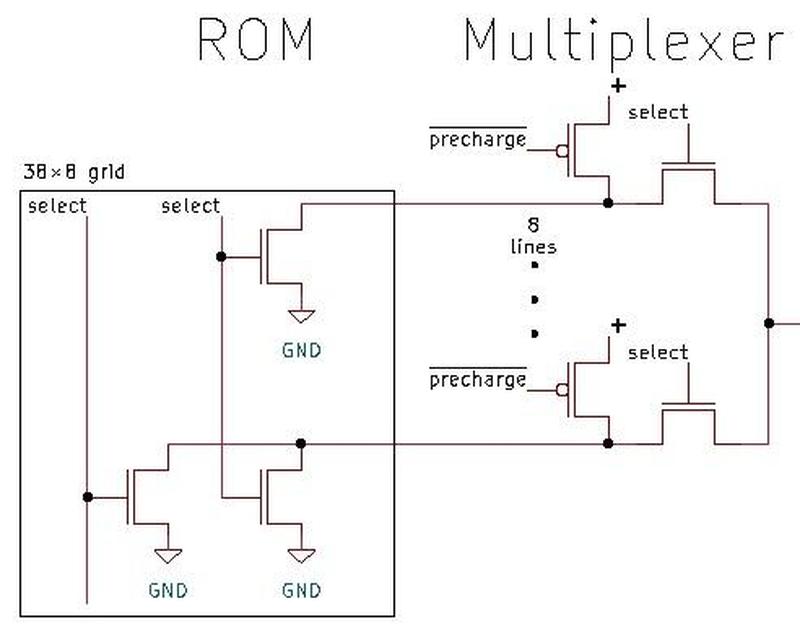
Cache memories are built from an array of memory storage elements in a structured grid,
visible in the rug as uniform pink rectangles.
The TLB (Translation Lookaside Buffer) assists the cache.
Finally, the "bus interface logic" connects the processor to the computer's bus, providing access to memory and peripheral
devices.
Around the edges of the physical chip, tiny bond pads provide the connections between the silicon chip and the integrated circuit package.
In the weaving, these tiny pads have been abstracted into small black rectangles.
The weaving is accurate enough to determine that it represents a specific Pentium variant, called P54C.
The motivation for the P54C was that
the original Pentium chips (called P5) were not as fast as hoped and ran hot.
Intel fixed this by using a more advanced manufacturing process, reducing the feature size from 800 to 600 nanometers
and running the chip at 3.3 volts instead of 5 volts.
Intel also modified the chip so that when parts of the chip were idle, the clock signal could be stopped to
save power. (This is the "clock driver" circuitry at the top of the weaving.)
Finally, Intel added multiprocessor logic (adding 200,000 more transistors), allowing two processors to work together more
easily.
The improved Pentium chip was smaller, faster, and used less power. This variant was called the P54C (for reasons I haven't
been able to determine).
The "multiprocessor logic" is visible in the Pentium rug, showing that it is the P54C Pentium (right) and not the P5 Pentium (left).

The Pentium P5 on the left and the P54C on the right, showing the difference in die and package sizes. If you look closely, the P5 die on the left lacks the "multiprocessor logic" in the weaving, showing that the weaving is the P54C. I clipped the pins on the P5 to fit it under a microscope.
Intel's connection with New Mexico started in 1980 when Intel opened a chip fabrication plant (fab) in Rio Rancho, a suburb north of Albuquerque.
At the time, this plant, Fab 7, was Intel's largest and produced 70% of Intel's profits.
Intel steadily grew the New Mexico facility, adding Fab 9 and then Fab 11, which opened in September 1995, building Pentium and Pentium Pro chips in a 140-step manufacturing process.
Intel's investment in Rio Rancho has continued with a $4 billion project underway for Fab 9 and Fab 11x.
Intel has been criticized for environmental issues in New Mexico, detailed in the book
Intel inside New Mexico: A case study of environmental and economic injustice.
Intel, however, claims a sustainable future in New Mexico, restoring watersheds, using 100% renewable electricity, and recycling construction waste.
Fairchild and Shiprock
Marilou Schultz is currently creating another weaving based on an integrated circuit, shown below.
Although this chip, the Fairchild 9040,
is much more obscure than the Pentium, it has important historical symbolism,
as it was built by Navajo workers at a plant on Navajo land.

Marilou Schultz's current weaving project. Photo provided by the artist.
In 1965, Fairchild started producing semiconductors in Shiprock, New Mexico,
about 200 miles northwest of Intel's future facility.
Fairchild produced a brochure in 1969 to commemorate the opening of a new plant. Two of the photos in that brochure compared a traditional Navajo weaving to the pattern of a chip, which happened to be the 9040.
Although Fairchild's Shiprock project started optimistically, it was suddenly
shut down a decade later after an armed takeover.
I'll discuss the complicated history of Fairchild in Shiprock and then describe the 9040 chip in more detail.

A Navajo rug and the die of a Fairchild 9040 integrated circuit. Images from Fairchild's
commemorative brochure on the opening of a new plant at Shiprock.
The story of Fairchild starts with William Shockley, who invented the junction transistor at Bell Labs, won the Nobel prize, and founded
Shockley Semiconductor Laboratory in 1957 to build transistors.
Unfortunately, although Shockley was brilliant,
he was said to be the worst manager in the history of electronics, not to mention a notorious eugenicist and racist later in life.
Eight of his top employees—called the "traitorous eight"—left Shockley's company in 1957 to found Fairchild Semiconductor.
(The traitorous eight included Gordon Moore and Robert Noyce who ended up founding Intel in 1968).
Noyce (co-)invented the integrated circuit in 1959 and Fairchild soon became a top semiconductor manufacturer, famous
for its foundational role in Silicon Valley.
The Shiprock project was part of an attempt in the 1960s to improve the economic situation of the Navajo through industrial development.
The Navajo had suffered a century of oppression including forced deportation from their land through the Long Walk (1864-1866).
The Navajo were suffering from 65% unemployment, a per-capita income of $300, and a lack
of basics such as roads, electricity, running water, and health care.
The Bureau of Indian Affairs was now trying to encourage economic
self-sufficiency by funding industrial projects on Indian land.4
Navajo Tribal Chairman Raymond Nakai viewed industrialization as the only answer.
Called "the first modern Navajo political leader", Nakai stated,
"There are some would-be leaders of the tribe calling for the banishment of industry from the reservation and a return to the life of a century ago! But, it would not solve the problems. There is not sufficient grazing land on the reservation to support the population so industry must be brought in."
Finally, Fairchild was trying to escape the high cost of Silicon Valley labor by opening plants in low-cost locations such as Maine, Australia, and Hong Kong.
These factors led
Fairchild to open a manufacturing facility on Navajo land in Shiprock, New Mexico.
The project started in 1965 with 50 Navajo workers in the Shiprock Community Center manufacturing transistors,
rapidly increasing to 366 Navajo workers.

Fairchild's manufacturing plant in Shiprock, NM, named after the Shiprock rock formation in the background. The formation is called
Tsé Bitʼaʼí in Navajo.
From
The Industrialization of a 'Sleeping Giant', Commerce Today, January 25, 1971.
By 1967, Robert Noyce, group vice-president of Fairchild, regarded the Shiprock plant as successful.
He explained that Fairchild
was motivated both by low labor costs and by social benefits, saying, "Probably nobody would
ever admit it, but I feel sure the Indians are the most underprivileged ethnic group in the United States."
Two years later, Lester Hogan, Fairchild's president,
stated,
"I thought the Shiprock plant was one of Bob Noyce's philanthropies until I went there," but he was so impressed that
he decided to expand the plant.
Hogan also directed Fairchild to help build hundreds of houses for workers; since a traditional Navajo dwelling is called a hogan,
the houses were dubbed Hogan's hogans.

In 1969, Fairchild opened its new facility at Shiprock and produced the commemorative brochure mentioned earlier.
As well as showing the striking visual similarity between the designs of traditional Navajo weavings and modern integrated circuits,
it stated that "Weaving, like all Navajo arts, is done with unique imagination and craftsmanship" and described
the "blending of innate Navajo skill and [Fairchild] Semiconductor's precision assembly techniques."
Fairchild later said that "rug weaving, for instance, provides an inherent
ability to recognize complex patterns, a skill which makes memorizing integrated circuit patterns a minimal problem."7
However, in Indigenous Circuits: Navajo Women and the Racialization of Early Electronic Manufacture,
digital media theorist Lisa Nakamura critiques this language as
a process by which "electronics assembly work became both gendered and identified with specific racialized qualities".5
Nakamura points out how "Navajo
women’s affinity for electronics manufacture [was described] as both reflecting and satisfying
an intrinsic gendered and racialized drive toward intricacy, detail, and quality."

At Shiprock, Fairchild employed 1200 workers,6 and all but 24 were Navajo, making Fairchild the nation's largest
non-government employer of American Indians. Of the 33 production supervisors, 30 were Navajo.
This project had extensive government involvement from the Bureau of Indian Affairs and the U.S. Public Health Service,
while the Economic Development Administration made business loans to Fairchild,
the Labor Department had job training programs, and Housing and Urban Development built housing at Shiprock7.
The Shiprock plant was considered a major success story at a meeting of the National Council on Indian Opportunity in 1971.7
US Vice President Agnew called the economic deprivation and
40-80% unemployment on Indian reservations "a problem of staggering magnitude" and encouraged more industrial development.
Fairchild President Hogan stated that "Fairchild's program at Shiprock has been one of the most rewarding in the history of our company, from the standpoint of a sound business as well as social responsibility."
He said that at first the plant was considered the "Shiprock experiment", but the plant
was "now among the most productive and efficient of any Fairchild operation in the world."
Peter MacDonald, Chairman of the Navajo Tribal Council and a World War II Navajo code talker, discussed the extreme poverty and unemployment on the Navajo reservation, along with "inadequate housing,
inadequate health care and the lack of viable economic activities."
He referred to Fairchild as "one of the best arrangements we have ever had" providing not only employment but also supporting
housing through a non-profit.

Navajo workers using microscopes in Fairchild's Shiprock plant. From "The Navajo Nation Looks Ahead", National Geographic, December 1972.
In December 1972, National Geographic highlighted the Shiprock plant as "weaving for the Space Age", stating that the Fairchild plant was the tribe's most
successful economic project with Shiprock booming due to the 4.5-million-dollar annual payroll. The article states: "Though the plant runs happily today, it was at first a battleground of warring
cultures."
A new manager, Paul Driscoll, realized that strict "white man's rules" were counterproductive.
For instance, many employees couldn't phone in if they would be absent, as they didn't have telephones.
Another issue was the language barrier since many workers spoke only Navajo, not English.
So when technical words didn't exist in Navajo, substitutes were found: "aluminum" became "shiny metal".
Driscoll also realized that Fairchild needed to adapt to traditional nine-day religious ceremonies.
Soon the monthly turnover rate dropped from 12% to under 1%, better than Fairchild's other plants.
Unfortunately, the Fairchild-Navajo manufacturing partnership soon met a dramatic end.
In 1975, the semiconductor industry was suffering from the ongoing US recession. Fairchild was especially hard hit,
losing money on its integrated circuits, and it shed over 8000 employees between 1973 and 1975.8
At the Shiprock plant, Fairchild laid off9 140 Navajo employees in February 1975, angering the community.
A group of 20 Indians armed with high-power rifles
took over the plant, demanding that
Fairchild rehire the employees.
Fairchild portrayed the occupiers, part of the AIM (American Indian Movement), as an "outside group—representing neither employees, tribal authorities nor the community."
Peter MacDonald, chairman of the Navajo Nation, agreed with the AIM on many points but viewed the AIM occupiers as "foolish" with "little sense of Navajo history" and "no sense of the need for an Indian nation to grow" (source).
MacDonald negotiated with the occupiers and the occupation ended peacefully a week later, with unconditional amnesty granted to the occupiers.10
However, concerned about future disruptions, Fairchild permanently closed the Shiprock plant and transferred production to Southeast Asia.

An article entitled "Navajos Occupy Plant". Contrary to the title, MacDonald stated that many of the occupiers were from other tribes and were not acting in the best interest of the Navajo. From
Workers' Power, the biweekly newspaper of the International Socialists, March 13-26, 1975.
For the most part, the Fairchild plant was viewed as a success prior to its occupation and closure.
Navajo leader MacDonald looked back on the Fairchild plant as "a cooperative effort that was succeeding for everyone" (link).
Alice Funston, a Navajo forewoman at Shiprock said, "Fairchild has not only helped women get ahead, it has been good
for the entire Indian community in Shiprock."11
On the other hand,
Fairchild general manager Charles Sporck had a negative view looking back:
"It [Shiprock] never worked out. We were really screwing up the whole societal structure of the Indian tribe.
You know, the women were making money and the guys were drinking it up.
We had a very major negative impact upon the Navajo tribe."12
Despite the stereotypes in Sporck's comments, he touches on important gender issues, both at Fairchild and in the electronics
industry as a whole.
Fairchild had long recognized the lack of jobs for men at Shiprock, despite attempts to create roles for men. In 1971, Fairchild President Hogan stated that
since "semiconductor assembly operation require a great amount of detail work with tiny components, [it] lends itself to
female workers. As a result, there are nearly three times as many Navajo women employed by Fairchild as men."7
The role of women in fabricating and assembling electronics is often not recognized.
A 1963 report on electronics manufacturing
estimated that women workers made up
41 percent of total employment in electronics manufacturing, largely in gendered roles.
The report suggested that
microminiaturization of semiconductors gave women an advantage over men in assembly and production-line work;
women made up over 70% of semiconductor production-line workers, with
90-99% of inspecting and testing jobs.
and 90-100% of assembler jobs.
Women were largely locked out of non-production jobs;
although women held a few technician and drafting roles, the percentage of woman engineers was too low to measure.
The defense contractor General Dynamics also had Navajo plants, but with more success than Fairchild.
General Dynamics opened a Navajo Nation plant in Fort Defiance, Arizona in 1967 to make missiles for the Navy.
At the plant's opening, Navajo Tribal Chairman Raymond Nakai pushed for industrialization, stating
that it was in "industrialization and the money and the jobs engendered thereby that the future of
the Navajo people will lie."
The plant started with 30 employees, growing to 224 by the end of 1969, but then dropping to 99 in 1971 due to
a slowdown in the electronics industry.
General Dynamics opened another Navajo plant near Farmington NM in 1988.
Due to the end of the Cold War,
Hughes Aircraft (part of General Motors) acquired General Dynamics' missile business in 1992 and sold it to Raytheon in 1997.
The Fort Defiance facility was closed in 2002 when its parent company, Delphi Automotive Systems, moved out of the military wiring business.
The Farmington plant remains open, now Raytheon Diné, building
components for Tomahawk, Javelin, and AMRAAM missiles.

Navajo workers at the General Dynamics plant in Fort Defiance, AZ. From the 1965 General Dynamics film "The Navajo moves into the electronic age". From
American Indian Film Gallery.
Inside the Fairchild 9040 integrated circuit
The integrated circuit die image in
Fairchild's commemorative brochure has an exceptionally striking design and color scheme.
It's clear why this chip brings weaving to mind.
Studying the die photo of the 9040 carefully reveals some interesting characteristics of integrated circuit design, so
I will go into some detail.

Die photo of the Fairchild 9040 flip-flop. From the commemorative brochure.
The chip was fabricated from a tiny square of silicon, which appears purple in the photograph.
Different regions of the silicon die were treated (doped) with impurities to change the properties of the silicon and thus create
electronic devices. These doped regions appear as green or blue lines.
The white lines are the metal layer on top of the silicon, connecting the components. The 13 metal rectangles
around the border are the bond pads.
The chip was packaged in an unusual 13-pin flat-pack, as shown below.
Each of the 13 bond pads above was connected by a tiny wire to one
of the 13 external pins.

The Fairchild 9040 packaged in a 13-pin flatpack integrated circuit. The chip was also available in a 14-pin DIP, a standard way of packaging chips. Photo from the commemorative brochure.
The Fairchild 9040 was introduced in the mid-1960s as part of Fairchild's Micrologic family, a set of high-performance
integrated circuits that were designed to work together.13
The 9040 chip was a "flip-flop", a circuit capable of storing a single bit, a 0 or 1. Flip-flops can be combined to
form counters, counting the number of pulses, for instance.
The most dramatic patterns on the chip are the intricate serpentine blue lines.
Each line forms a resistor, controlling the flow of electricity by impeding its path.
The lines must be long to provide the desired resistance, so they wind back and forth to fit into the available space.
Each end of a resistor is connected to the metal layer, wiring it to another part of the circuit.
Most of the die is occupied by resistors, which is a disadvantage of this type of circuit. Modern integrated circuits
use a different type of circuitry (CMOS), which is much more compact, partly because it doesn't need bulky resistors.

Resistors in the 9040 die.
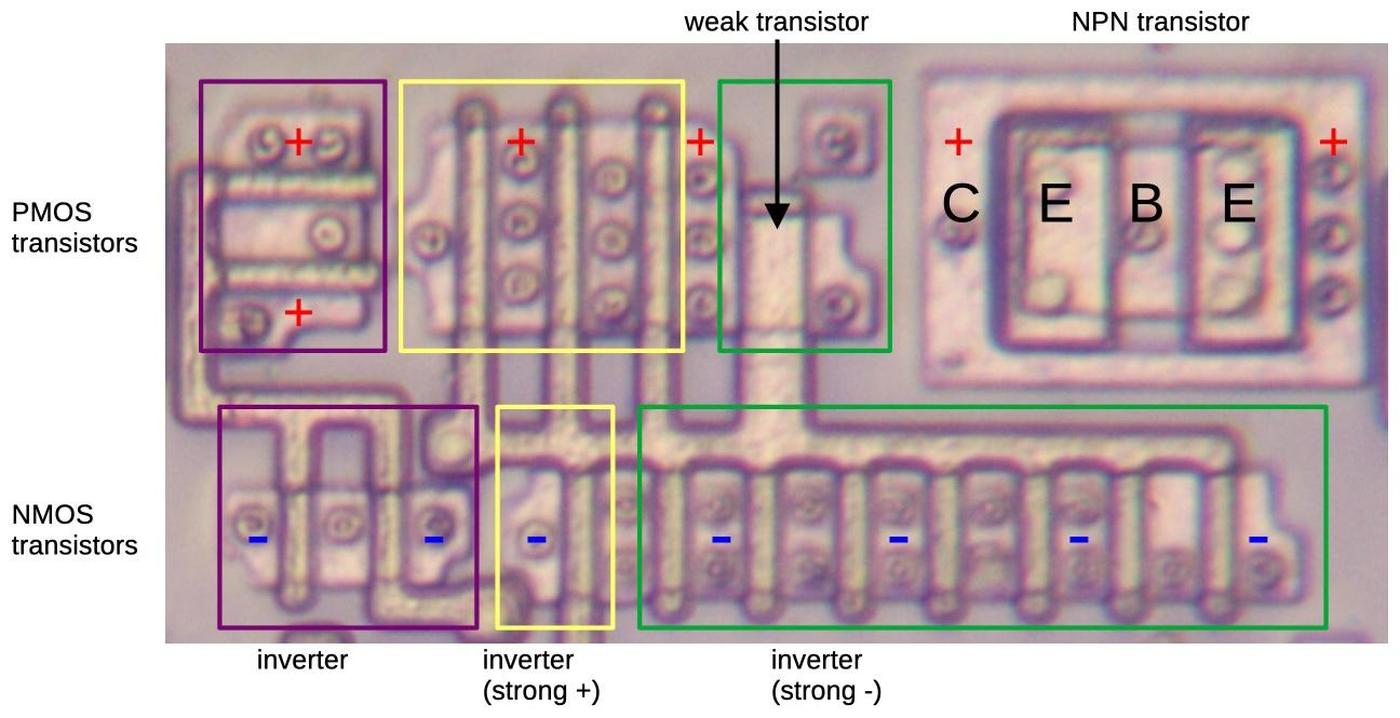
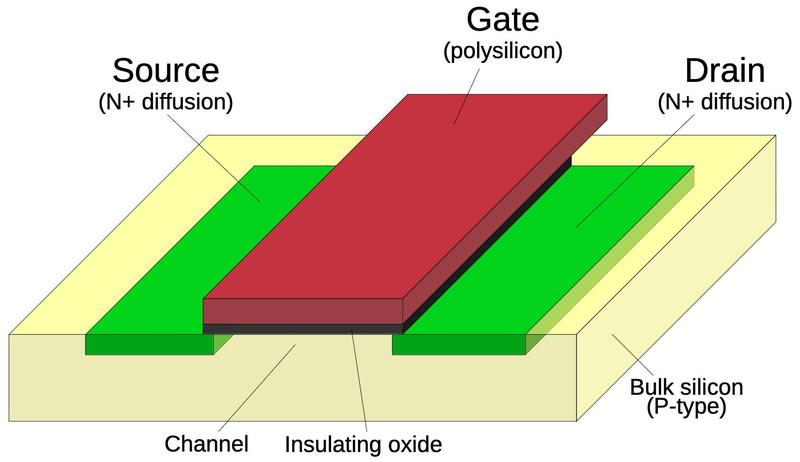
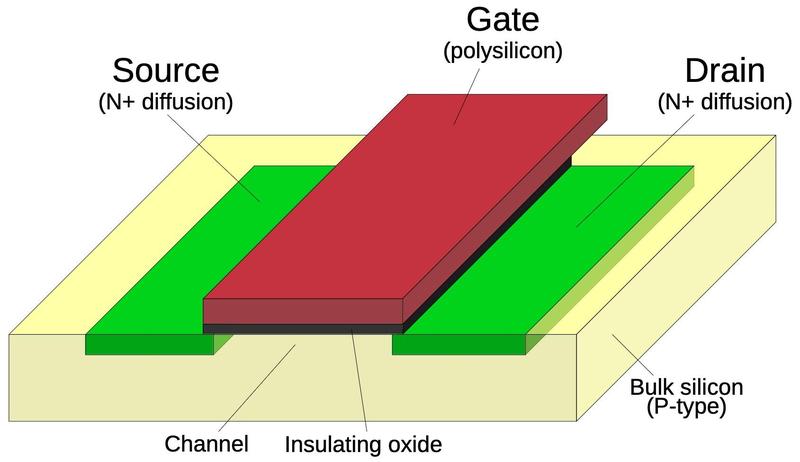
Transistors are the main component of an integrated circuit. These tiny devices act as switches, turning signals on and off.
The photo below shows one of the transistors in the 9040.
It consists of three layers of silicon, with metal wiring connected to each layer. Note the blue region in the middle,
surrounded by a slightly darker purple region; these color changes indicate that the silicon has been doped to change
its properties.
The green region surrounding the transistor provides isolation between this transistor and the other circuitry, so
the transistors don't interfere with each other.
The chip also has many diodes, which look similar to transistors except a diode has two connections.

A transistor in the 9040 die. The three contacts are called the base, emitter, and collector.
These transistors with their three layers of silicon are a type known as bipolar.
Modern computers use a different type of transistor, metal-oxide-semiconductor (MOS), which is much more compact and
efficient.
One of Fairchild's major failures was staying with bipolar transistors too long, rather than moving to MOS.14
In a sense, the photo of the 9040 die shows the seeds of Fairchild's failure.
The 9040 chip was constructed on a completely different scale from the Pentium, showing the rapid progress of the IC industry.
The 9040 contains just 16 transistors, while the Pentium contains 3.3 million transistors.
Thus, individual transistors can be seen in the 9040 image, while only large-scale functional blocks are visible in the Pentium.
This increasing transistor count illustrates the exponential growth
in integrated circuit capacity between the 9040 in the mid-1960s and the Pentium in 1993.
This growth pattern, with the number of transistors doubling about every two years, is known as Moore's law, since it
was first observed in 1965 by Gordon Moore (one of Fairchild's "traitorous eight", who later started Intel).
The schematic below shows the circuitry inside the 9040 chip, with its
16 transistors, 16 diodes, and 22 resistors.
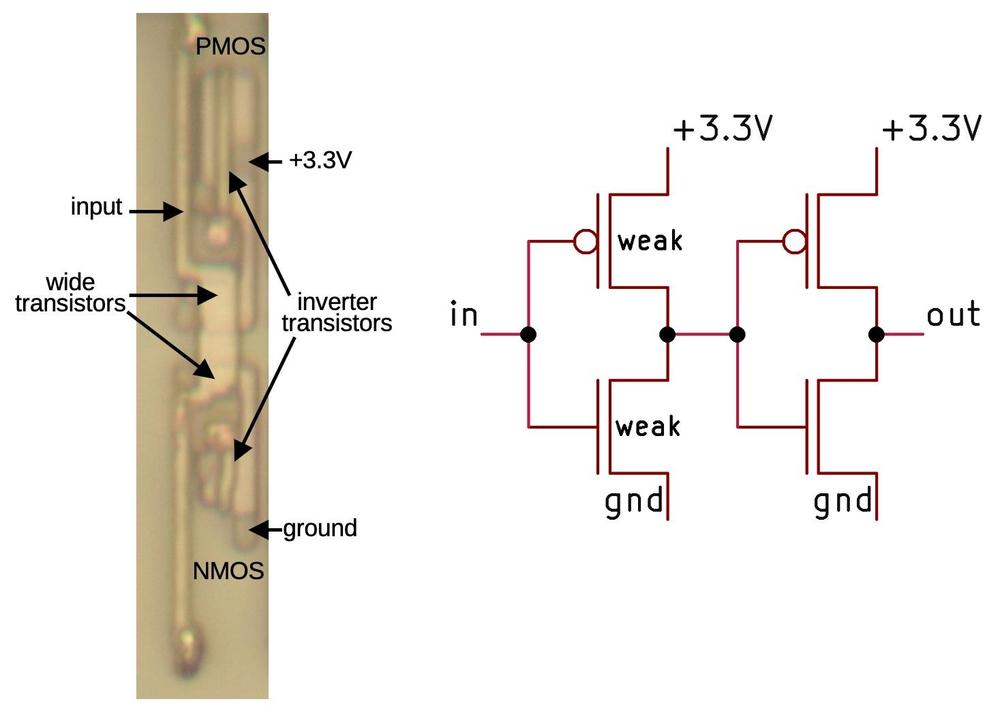
The symmetry of the 9040 die photo makes it appealing, and that symmetry is reflected in the circuit below, with the left side and
the right side mirror images.
The idea behind a flip-flop is that it can hold either a 0 or a 1. In the chip, this is implemented by turning on the
right side of the chip to hold a 0, or the left side to hold a 1. If one side of the chip is on, it forces the other side
off, accomplished by the X-like crossings of signals in the center.15
Thus, the symmetry is not arbitrary, but is critical to the operation of the circuit.
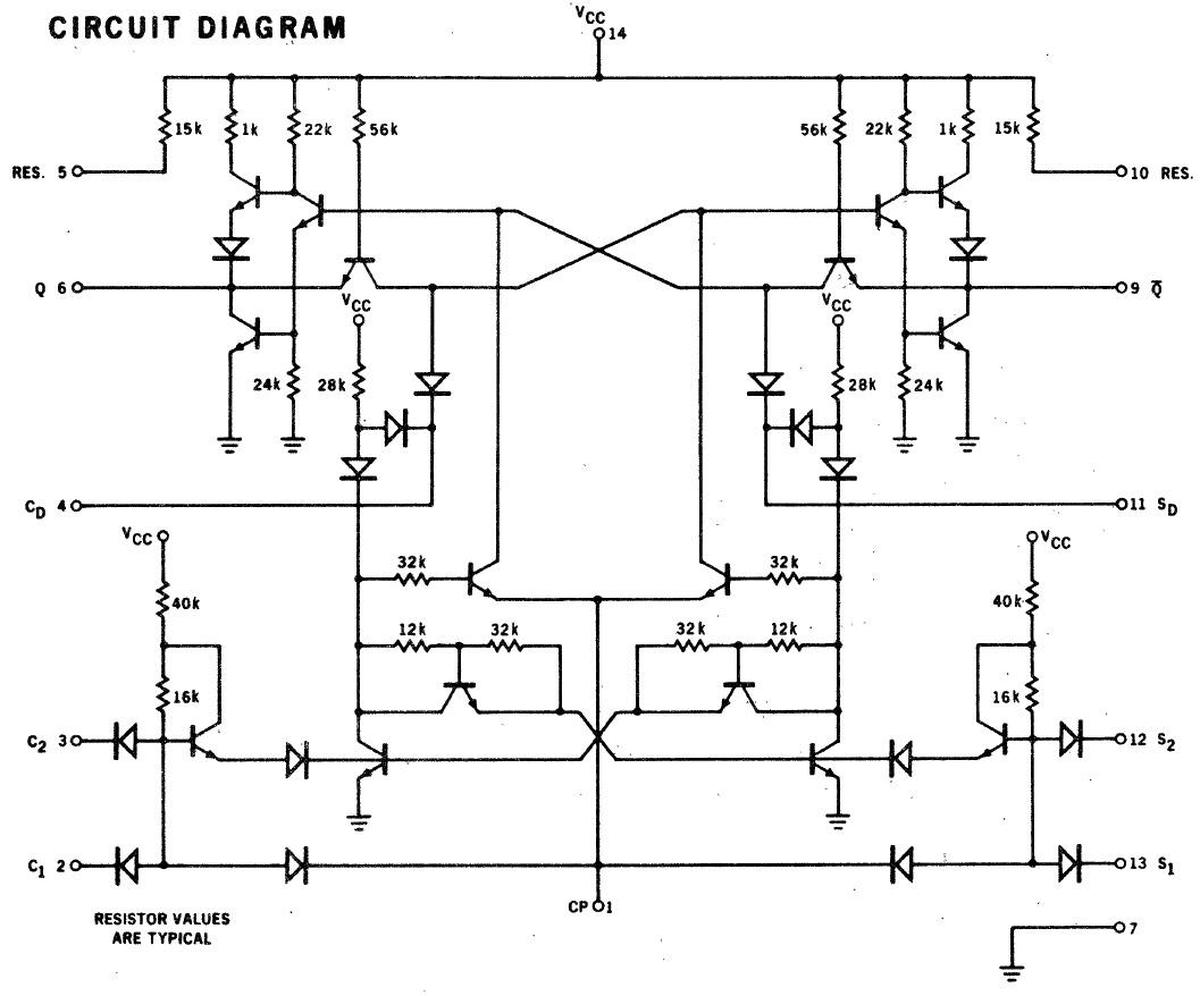
Despite the obscurity of the 9040, multiple 9040 chips are currently on the Moon.
The chip was
used in the Apollo Lunar Surface Experiments Package (ALSEP),16
in particular, the Active Seismic Experiment on Apollo 14 and 16. This experiment detonated small explosives on the Moon
and measured the resulting seismic waves.
The photo below is a detail from a blueprint17
that shows three of the nineteen 9040 flip-flops (labeled "FF") as well as two 9041 logic gates, a chip in the same family
as the 9040.
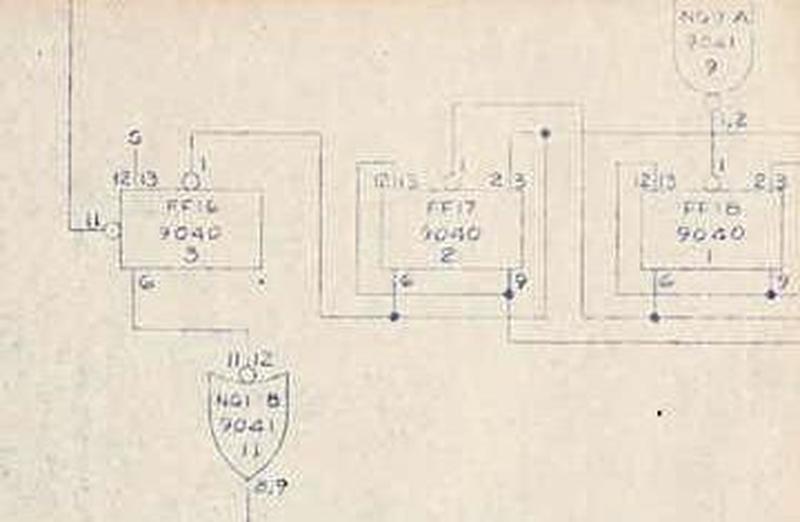
Detail from Logic Schematic Type B Board No.4 ASE.
Conclusions
The similarities between Navajo weavings and the patterns in integrated circuits have been described since the 1960s.
Marilou Schultz's weavings of integrated circuits make these visual metaphors into concrete works of art.
Although the Woven Histories exhibit at the National Gallery of Art is no longer on display,
the exhibit will be at the National Gallery of Canada (Ottawa) starting November 8, 2024, and the Museum of Modern Art (New York)
starting April 20, 2025
(full dates here).
If you're in the area, I recommend viewing the exhibit, but don't make my mistake: leave more than
five minutes to see it!
Many thanks to Marilou Schultz for discussing her art with me.
For more on her art, see A Conversation with Marilou Schultz on YouTube.18
Follow me on Mastodon as @kenshirriff@oldbytes.space
or RSS for updates.
Notes and references
-
The original Pentium was followed by the Pentium Pro, the Pentium II, and others, forming a long-running brand of high-performance processors. Pentium was Intel's flagship line until the Core processors took over in 2006. ↩
-
Sheep hold a key role in Navajo culture and economy, which I'll briefly summarize here.
Domestic sheep were brought to the Americas during the Spanish colonization, reaching the Navajo in the late 1500s.
Since sheep were able to graze on semi-arid land unsuitable for crops, sheep became very important to the Navajo.
Although the Navajo had used cotton for weaving in the past, the availability of wool made weaving a fundamental industry;
the production and trading of woven Navajo blankets became an important economic factor in New Mexico by
the 1750s
(details).
Navajo leader Peter MacDonald described the role of sheep: "Sheep were like money in the bank: the more you had, the better your life, your future, and your family's future."
The number of sheep grew exponentially in the early 1900s, resulting in overgrazing of the land.
The drought and Dust Bowl of the 1930s led the government to restrict the number of sheep on Navajo land, imposing the
Navajo Livestock Reduction.
This heavy-handed program purchased and slaughtered over half the livestock, which was catastrophic to the Navajo, both
economically and culturally, destroying the Navajo's wealth and self-sufficiency.
The Navajo-Churro sheep is a breed that the Navajo developed from the
Churra sheep brought from Spain during the Spanish colonization of the Americas.
These sheep have a long, lustrous fleece that is excellent for weaving.
The Navajo-Churro is also called the Navajo Four-Horned Sheep as some rams have four horns, a rare trait.
The Navajo-Churro breed was severely depleted when American troops killed livestock during the Navajo Wars (1863)
and then brought close to extinction by the Livestock Reduction of the 1930s to 1950s.
In the 1970s, the Navajo Sheep Project started efforts to preserve
and revitalize the Navajo-Churro. The breed is still rare, but currently numbers in the thousands.
Now, climate change and water shortages are putting more pressure on sheep grazing. ↩
-
A photo of the rug was published in American Indian Science & Engineering Society 1994 Annual Report.
This photo shows the "physically accurate" side of the rug, not the side that is currently on display.

A photo of the rug from 1994.
Which side of a die image is the top is mostly arbitrary. Intel usually presents die photos with the tiny text on the die right
side up, so I will use that convention.
For the Pentium die, this text is in the lower right corner and says "80P54C (m) (c) intel '92,'93".
Of course, this text is much too small to be part of the woven rug. ↩
-
Strengthening the Indian Economy (Indian Affairs, 1966)
discusses various industrial development projects, of which Fairchild was the largest. Other projects included
a plant at Rolla, ND to produce sapphire and ruby bearings, a Seminole project with Amphenol to produce electronic connectors,
and a Hopi project with BVD to produce garments.
Other economic development projects included timber and mining; extractive industries provided over half of Navajo income. ↩
-
Racialization is defined by Nakamura as "the understanding of a specific population as possessing traits and behaviors that belong to a race, not an individual." ↩
-
Many photos of workers at the Shiprock plant are in Fairchild VIEWS, March 1969. Fairchild deserves credit for referring to the workers by name rather than
viewing them as anonymous props for photos.
Fairchild followed the same practice in its annual reports. ↩
-
NCIO (National Council on Indian Opportunity) News, Oct/Nov 1971 described
a high-level meeting with industry to discuss "new development on Indian reservations" with industry.
US Vice President Spiro Agnew ran the meeting, with Attorney General John Mitchell a speaker along with Navajo Tribal Council
chairman Peter MacDonald.
Bizarrely, all three ended up convicted of felonies for different reasons.
Within a few years, Mitchell was imprisoned for Watergate crimes and Agnew pled guilty to federal tax evasion.
In 1990, MacDonald was convicted of fraud, riot, extortion, racketeering, and conspiracy by a Navajo tribal judge and then a federal judge, spending
eight years in prison until pardoned by Bill Clinton (details).
The story of Peter MacDonald is complex and many view his prosecution as politically motivated;
MacDonald's memoir provides his perspective. ↩↩↩↩
-
Although Fairchild was highly successful at first, it suffered from chaotic management and economic decline.
Fairchild steadily lost key employees, many of whom started competing companies.
Most important was Intel, started in 1968 by Moore and Noyce, two of the "Traitorous Eight".
Eventually, hundreds of companies
(called the Fairchildren)
could be traced back to Fairchild.
Economic factors also battered Fairchild; the semiconductor industry had barely recovered from the 1970-1971 recession
when it was hit by the severe 1975 recession.
As a result, Fairchild had large layoffs, of which the Shiprock layoffs were a small part.
Fairchild's business continued to decline; it was purchased by Schlumberger in 1979 and went through various acquisitions, mergers, and spinoffs until it finally ended in 2016, acquired by ON Semiconductor. ↩
-
Were the employees "laid off" or "layed off"? Curiously, the New York Times article said "layed off" but sources uniformly state that "layed off" is grammatically wrong.
The New York Times has extensively used
"layed off" so this isn't a one-time typo.
I hypothesized that usage had changed since the 1970s but Google Ngram Viewer shows laid off as the consistent and overwhelming winner.
Maybe "layed off" was a stylistic quirk of the New York Times? ↩
-
Looking back, MacDonald questioned his decision
to let the occupation of Fairchild's plant continue rather than ordering the tribal police to forcibly remove the occupiers from
the plant.
In his view, his decision to let the occupation led to the closing of the plant and the loss of 1200 jobs.
On the other hand, forcibly removing the occupiers risked violence and loss of life: "I would have become the chairman who
killed his own people instead of the chairman who allowed Navajo to lose their jobs."
The risk of bloodshed was not theoretical. In 1989, a riot between
MacDonald's supporters and the police resulted in two Navajos being shot and killed by the police.
MacDonald pressed for a federal investigation into police brutality, but instead MacDonald and Benally (a council delegate)
received long prison sentences for inciting the riot even though they were not present at the time. ↩
-
Alice Funston was Forewoman for the Reliability and Quality
Assurance Section at Shiprock. In a Fairchild employee newsletter, she said, "Fairchild has not only helped
women get ahead, it has been good
for the entire Indian community in
Shiprock. Before the plant was built
here, there weren't many jobs available. You could work for the Bureau
of Indian Affairs, the Navajo Tribe or
other government agencies, but there
just weren't enough jobs to go around.
I started in assembly in 1965 and
was recently promoted to Production
Supervisor in R & Q.A. Since the beginning of the year, a number of
women have been promoted into
supervisory positions. When I joined
Fairchild, most of the members of
management were non-Indian. Today,
almost all of our supervisors and
managers are Indian."
I quote this at length, since it was the only example I could find of an employee discussing Shiprock in their own words.
It must be recognized, of course, that this is a company publication, so the comments may not be completely candid.
See "Affirmative Action: A growing consciousness of the needs of the individual" in Fairchild HORIZONS,
May-June, 1973. ↩
-
See Interview with Charlie Sporck, 2000 February 21, timestamp 0:27.
From "Silicon Genesis: oral history interviews of Silicon Valley scientists, 1995-2024," Stanford Digital Repository.
I view Sporck's comments on the failure of Shiprock as highly questionable.
First, Sporck left Fairchild in 1967, so he was not present for most of the Shiprock project. Moreover,
he implies that Fairchild's closing of Shiprock was in the best interest of the Navajo, which is a morally convenient
justification for Fairchild's decision, but contradicted by most other sources. ↩
-
Fairchild's 9040 logic family was called LPDTμL for "low-power diode-transistor Micrologic".
Some sources label
this family as TTL (Transistor-Transistor Logic), probably confusing it with the 9000-family, which was TTL. ↩
-
Fairchild's failure to recognize the importance of MOS transistors and transition from bipolar transistors is
described in History of Semiconductor Engineering, page 170. ↩
-
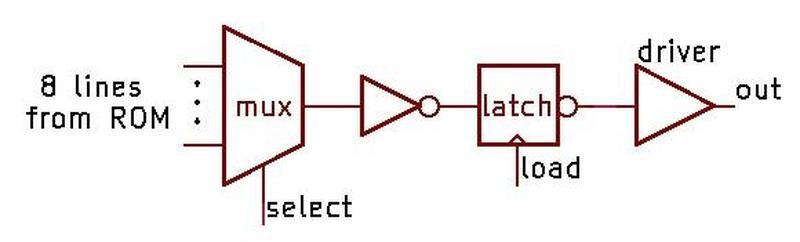
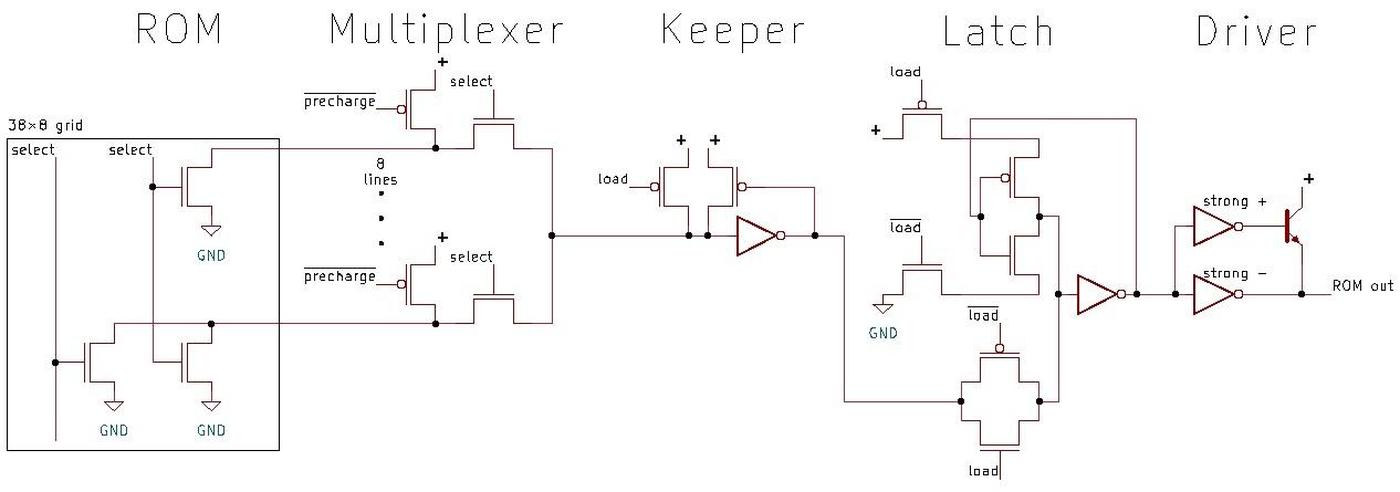
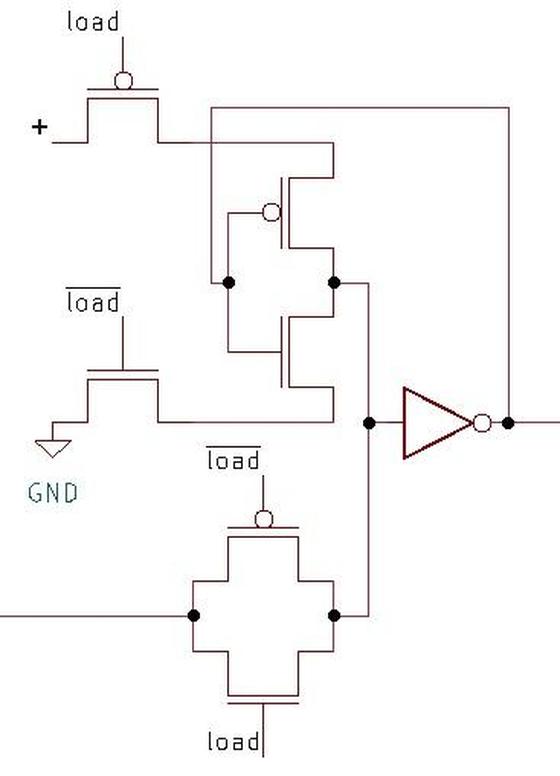
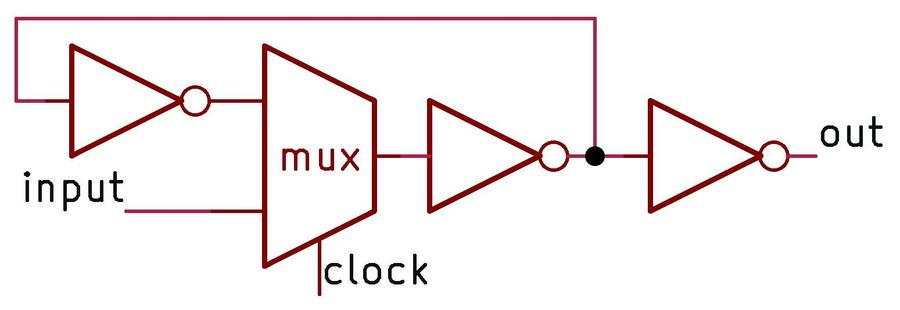
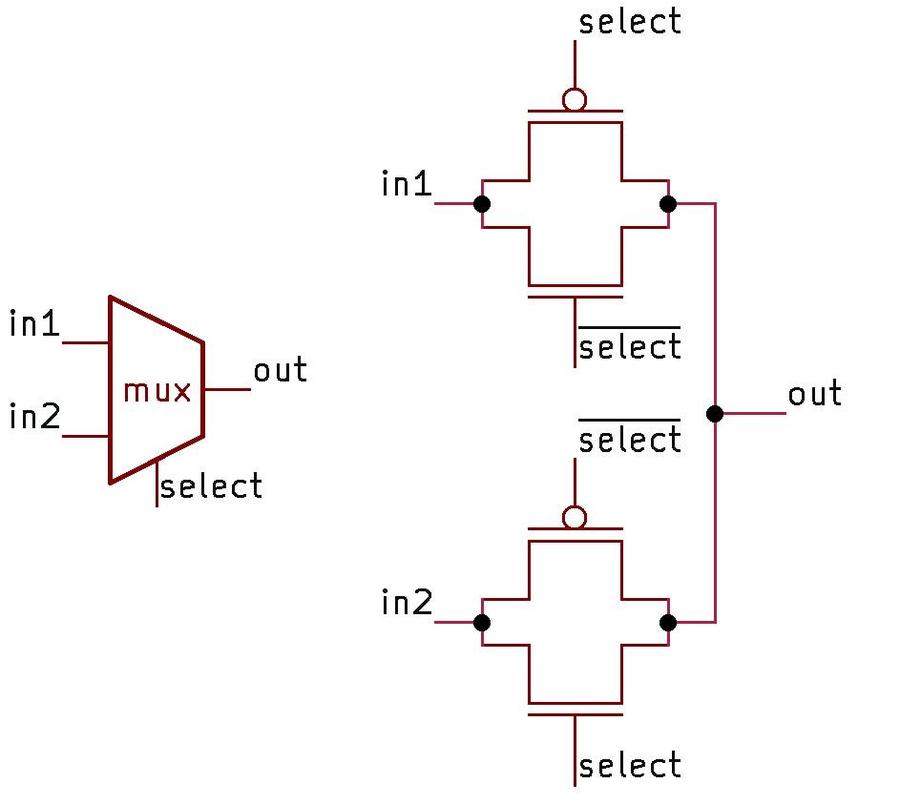
I'll provide more details of the 9040 schematic in this footnote.
The 9040 is a flexible flip-flop. It can be wired as an R-S (reset-set) flip-flop, set to 1 or reset to 0 as needed.
It can also be wired as a J-K flip-flop, a flexible circuit that can store a value, hold a value, or toggle, based on
the settings of the J and K inputs.
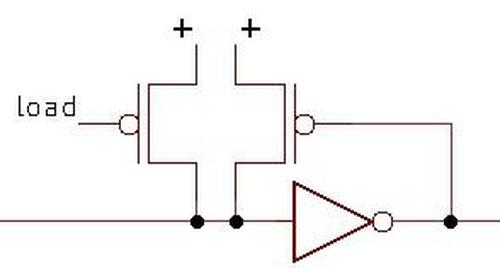
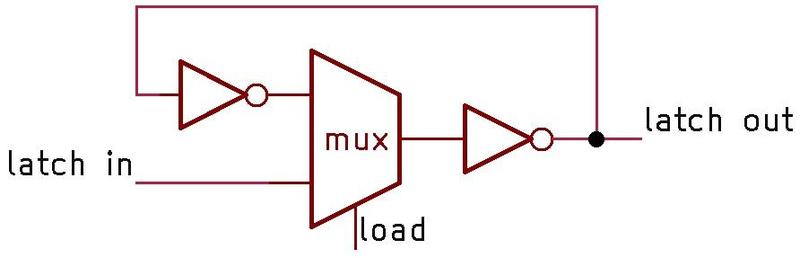
The 9040 is a "dual-rank" flip-flop, meaning it holds its
value in two latches: a primary latch and a secondary latch.
(This type of flip flop was generally called "master-slave", a name that is now controversial).
Looking at the schematic, the primary latch at the bottom of the schematic passes its value to the secondary
latch at the top under the control of the clock.
This structure makes the flip-flop "edge-triggered", changing its value at the moment when the clock signal changes.
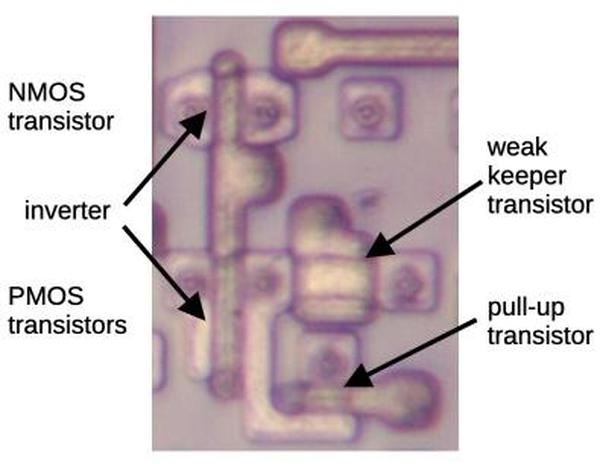
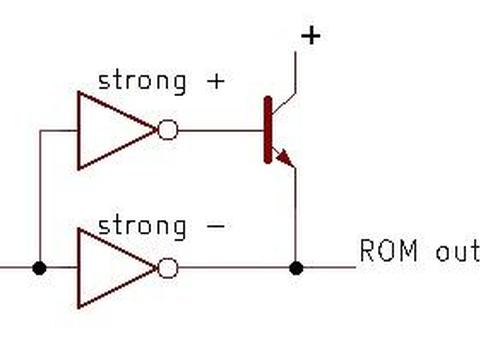
This circuit uses diode-transistor logic. Diodes perform most of the logic operations by combining input signals, while
the transistors provide amplification. Diodes play a different role in the "push-pull" output circuit, raising the
level of the high-side transistor.
Because the output circuit has a transistor, diode, and transistor stacked vertically, it is often called a
totem pole output,
a name that seems questionable in this context.
One curious feature of the 9040 is that it contains two pull-up resistors that are not assigned any role. The user
of the chip can attach them to unused inputs to keep the input at the desired value.
Looking at the schematic shows 13 pins, corresponding to the 13 pins of the flat-pack integrated circuit. All but
three of these pins are symmetrical; power (Vcc), ground, and the clock (CP) have single connections. The ground pad
is in the bottom-center of the die, which maintains symmetry. The clock and power pads are side-by-side in the top-center
of the die. If you study the die photograph closely, you will see that they subtlely break the chip's symmetry as the
clock signal runs down the center of the die while the power connection runs down both sides.
There are a few other subtle violations of symmetry when signals cross from one side of the chip to the other, as well as
the obviously asymmetrical text. ↩
-
I haven't been able to prove that the Apollo program used chips from the Shiprock plant rather than a different facility.
Fairchild President Hogan stated that workers at Shiprock assembled guidance,
communications, and gyro systems that were used on Apollo rockets. ↩
-
The ALSEP schematic is from Miller, K. Logic Schematic Type B Board No.4 ASE, A4, technical drawing, January 27, 1967, University of North Texas Libraries, The Portal to Texas History; crediting Lunar Planetary Institute Library. ↩
-
Marilou Schultz had another chip weaving on display at the National Gallery of Art. It is labeled "Untitled (Unknown Chip), 2008", but Antoine Bercovici identified it for me as the AMD K6 III processor, released in 1999 and comparable to the Pentium III.

A weaving created by Marilou Schultz, "Untitled (Unknown Chip)".
If you're interested in computer-related weaving, the exhibition also had "Copper Tapestry (Riva 128 Graphics Card, Nvidia, 1997)" by Argentinian artist Analia Saban, created
on a computer-automated Jacquard loom.
This weaving represents a PC graphics card, specifically, the STB Velocity 128, which uses the Nvidia Riva 128 GPU chip.
This chip was released in 1997, at a point when Nvidia was in a dire financial position, thirty days from going out of business.
The Riva 128 saved Nvidia and now Nvidia is the world's third most valuable company.

A tapestry created by Analia Saban, "Copper Tapestry (Riva 128 Graphics Card, Nvidia, 1997)".
↩